Here’s a video of the new Limited Logic Inspector (LLI) in action. The LLI Edition of BPC Logic Filter is for those MS Project users looking to examine the schedule logic network, but without a need for advanced analysis or reporting of logic flow. It’s pretty smooth.
Multiple Critical Paths – Revisited with BPC Logic Filter
While writing an article on Multiple Critical Paths a few years ago, I knew that BPC Logic Filter (our add-in for Microsoft Project) could easily identify multiple critical paths (and near-critical paths) in any project schedule, but we needed to analyze key milestones one at a time. In most cases I think that’s still the best approach to understanding the factors that drive (and may delay) key project deliverables. Nevertheless, the latest build of the software (1.5.5.13) includes a new setting that facilitates simultaneous analysis and display of the critical paths to multiple milestones in a project or program schedule.
The setting – Group Results by Selected Task – is found on the Tracing Preferences tab of the software settings, and we enabled it as part of the initial distribution of the build. We hope that at least a couple users have been pleasantly surprised.
This short article provides a couple illustrations of the feature in action.
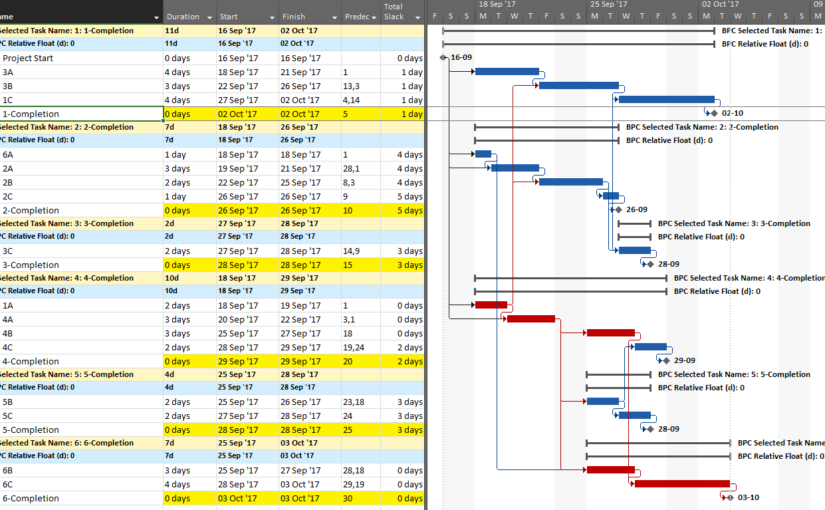
First, here is the simple example project from the previous article. The project comprises six “phases” of inter-related tasks in a Microsoft Project schedule, now displayed using MSP 2016 rather than MSP 2010 as before. The project has no deadlines or constraints, and MSP designates critical tasks (red bars in the chart) based on total slack (TS<=0).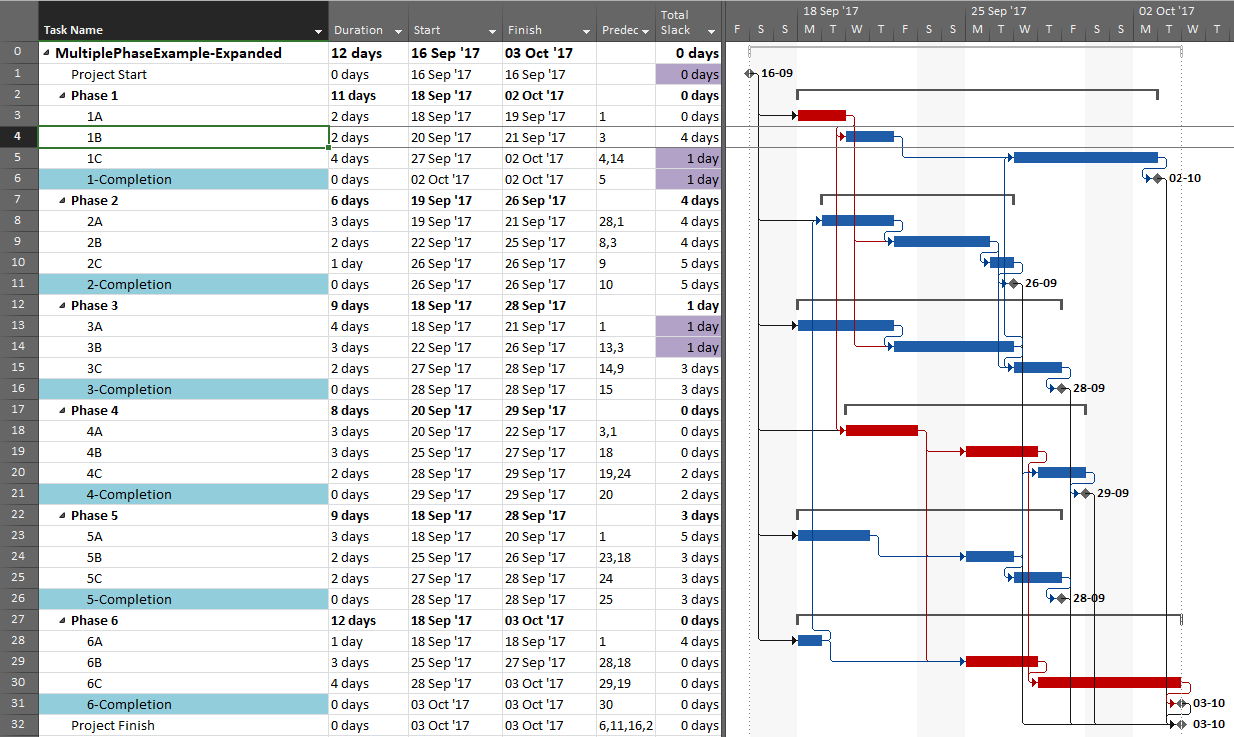
In the previous article, I illustrated – using MSP and Oracle P6 – several generic techniques to identify the unique critical path for each of the six phase completion milestone in the project. I also used BPC Logic Filter to graphically illustrate the critical- and near-critical paths for the Phase 1 completion milestone, displayed within the context of the overall project (and repeated here in MSP 2016).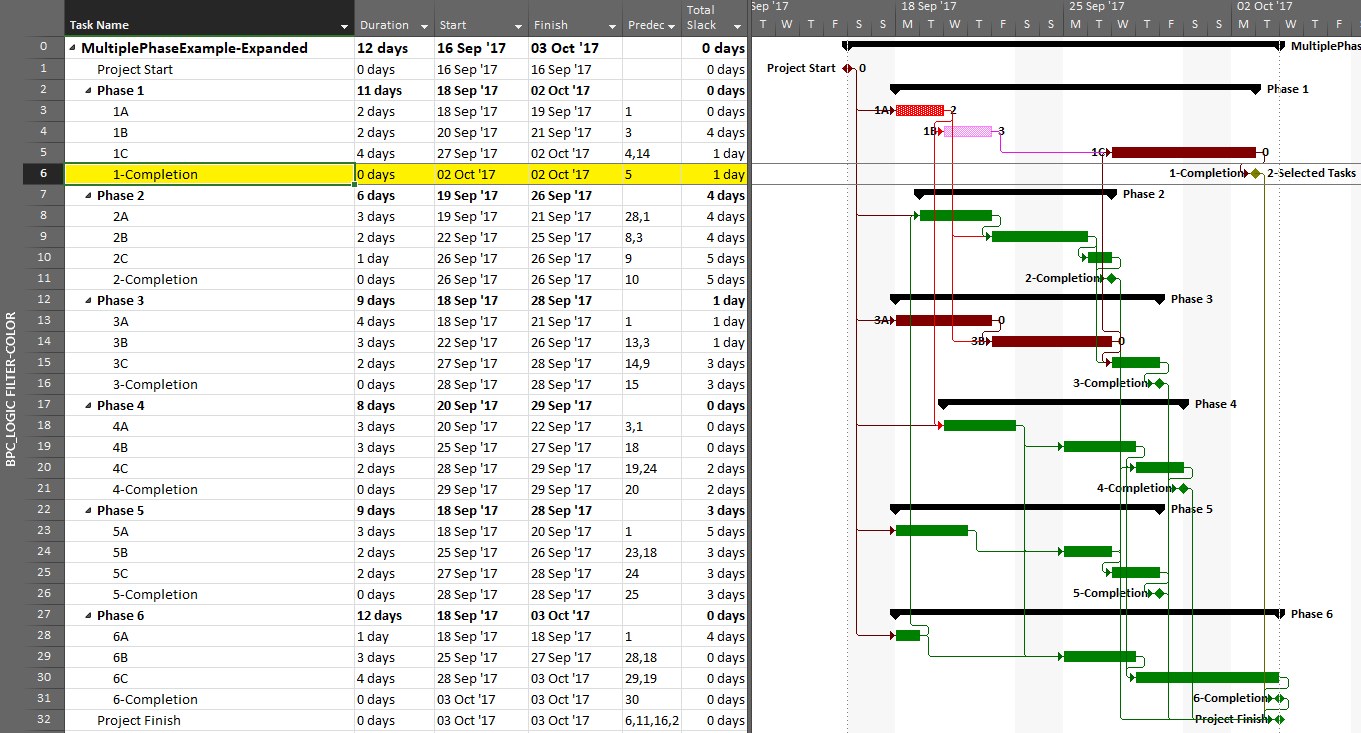
Going back to the original project, we can now run the task logic tracer with all six phase-completion milestones selected. The Standard Edition of BPC Logic Filter then allows us to select driving-path predecessors and to re-sort the results to show logical branches (i.e. paths).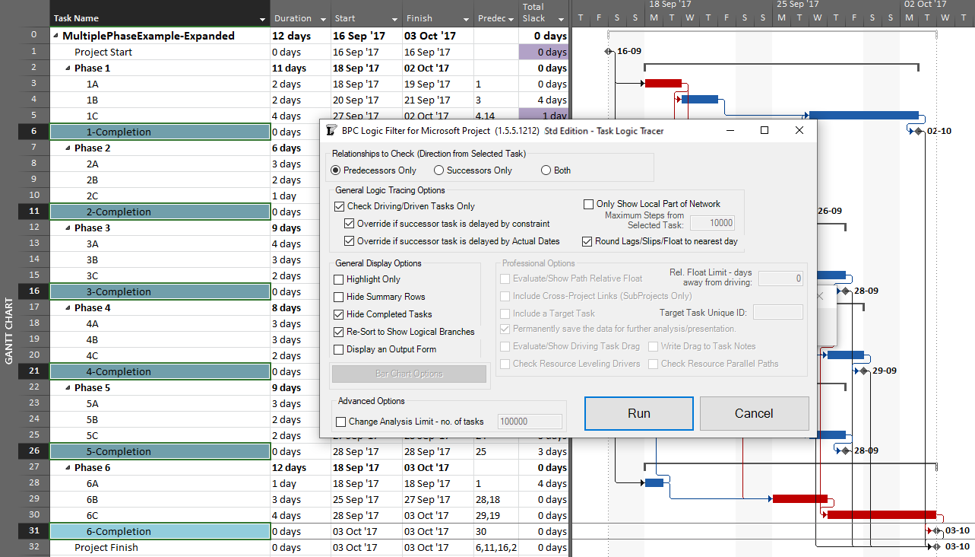
The result is a grouped view displaying the driving predecessor path to each of the six phase-completion milestones.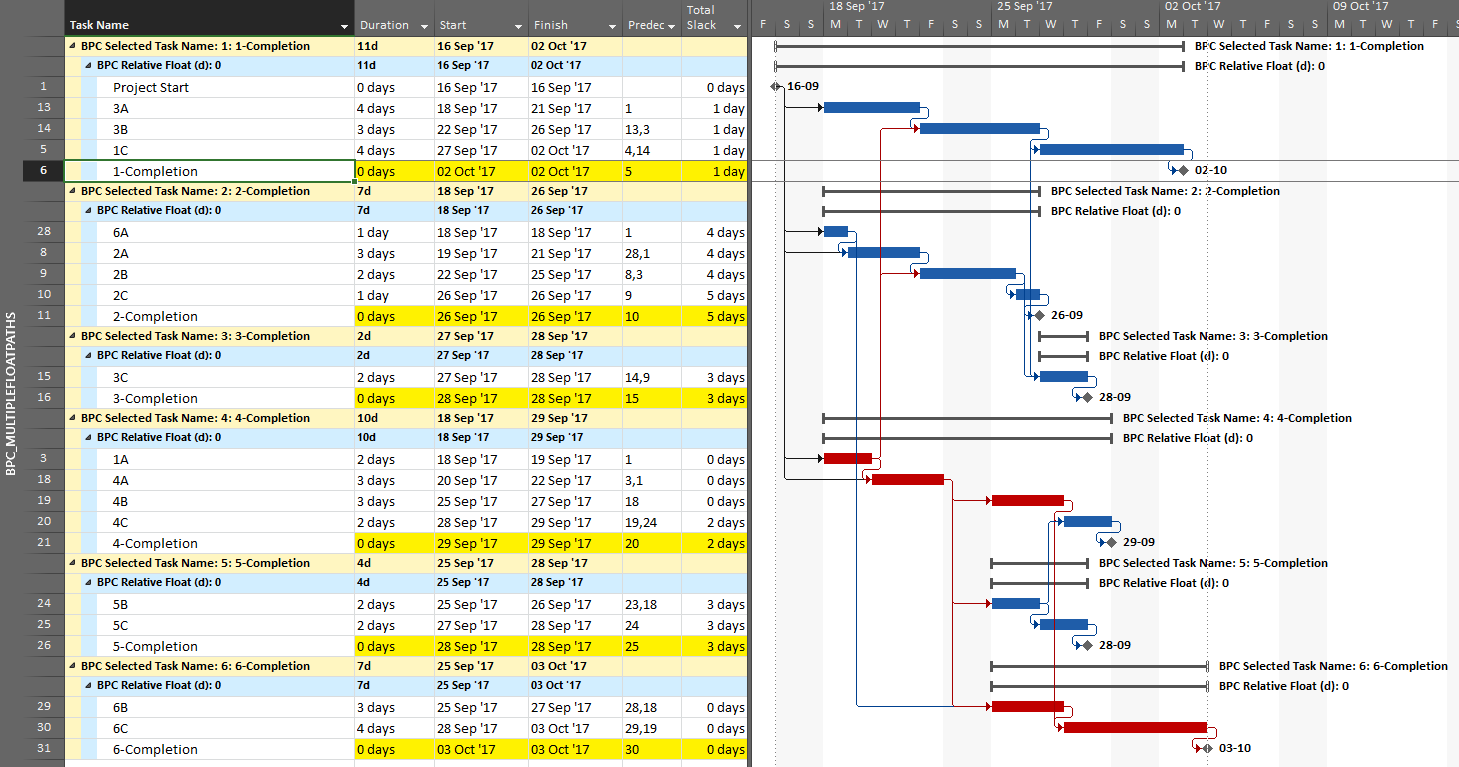
Due to intersecting logic, some tasks are on the driving/critical path for more than one completion milestone, but the Gantt chart only allows them to be displayed once. The task logic tracer displays such tasks together with the driven milestone that is encountered first in the original task selection. Thus, while tasks 1A, 4A, and 4B are critical for the overall project and for the phase-6 completion, they are displayed with the phase 4 completion milestone – for which they are also driving/critical – because that milestone was encountered first in the user’s selection. As a consequence, re-sorting the tasks in the overall project can alter the apparent driving paths for key delivery milestones when intersecting logic is present.
The same caveat applies when considering near-driving/critical paths for multiple key milestones in the same project, along with an added condition that a non-driving task will be included with whichever key milestone it is nearest to driving. To illustrate, we have re-run the previous analysis while considering path relative float, and we’ve decided to re-color bars to clarify results.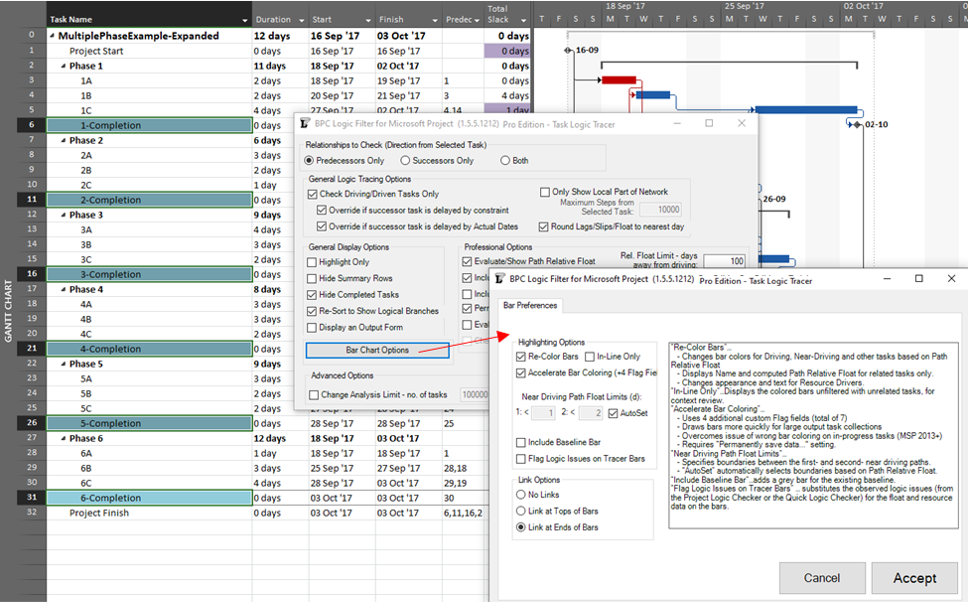
The resulting output is like the earlier one, but now including annotated bars and tasks whose path relative float is above zero (i.e. non-driving).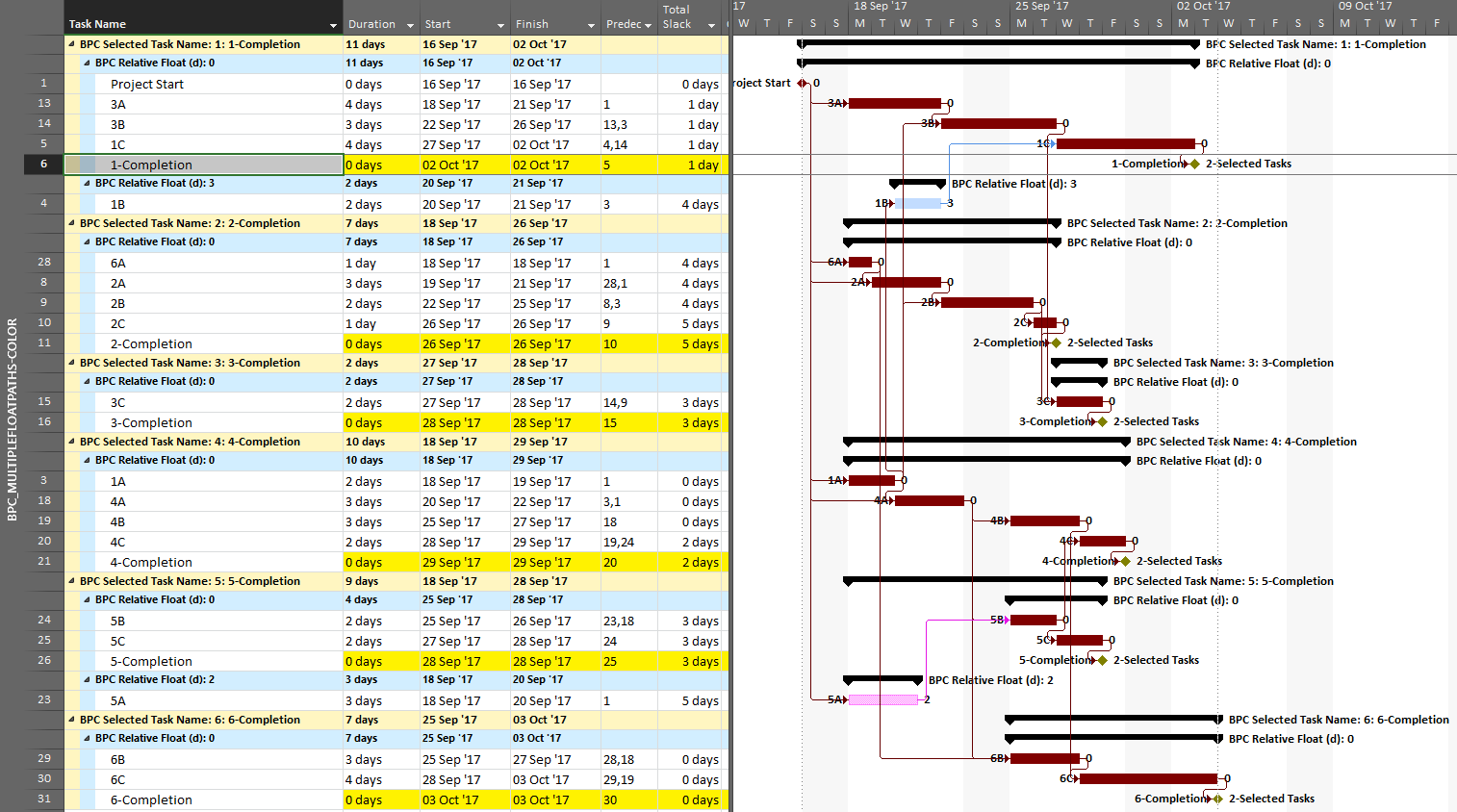
From the earlier article, we already know that task 1A is a non-driving path predecessor of the phase-1 completion milestone, 2 days from driving that milestone. It is nearer to driving (and is in fact driving) the phase-4 completion, however, so that is where it is shown.
As we’ve seen, it can be difficult to differentiate the critical paths to multiple completion milestones in a complex project with lots of intersecting logic paths. When a project or program includes multiple completion phases that are not closely related, however, the output is straightforward. A good example of this case occurs when multiple unrelated subprojects are combined into a linked master project for reporting purposes. Here I’ve used the New Window dialog to temporarily combine three simple projects into a temporary master. Then I have applied a filter to show only the key completion milestones for the three subprojects. Finally. I’ve run the task logic tracer with all the visible tasks selected. A Pro Edition of the tool is required to analyze linked subprojects, and I’ve limited the relative float analysis to keep the resulting output small.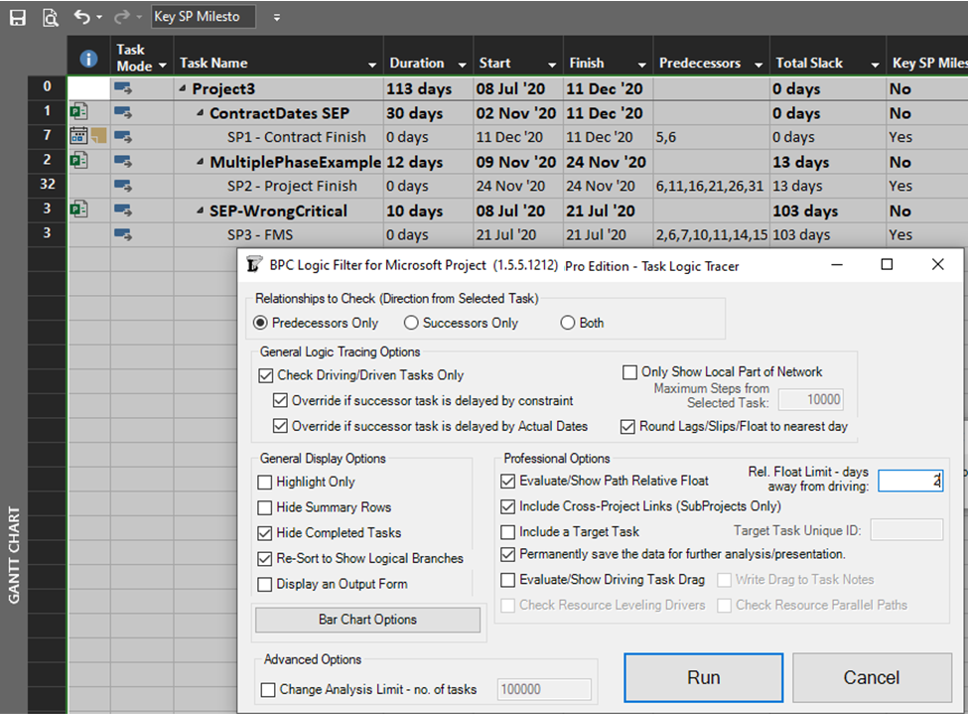
The resulting layout clearly depicts the critical/driving- and near-critical/driving paths for each subproject completion milestone. As usual – for BPC Logic Filter – the definitions of critical/driving logic paths do not rely on the total slack, which is not reliable in many modern project schedules.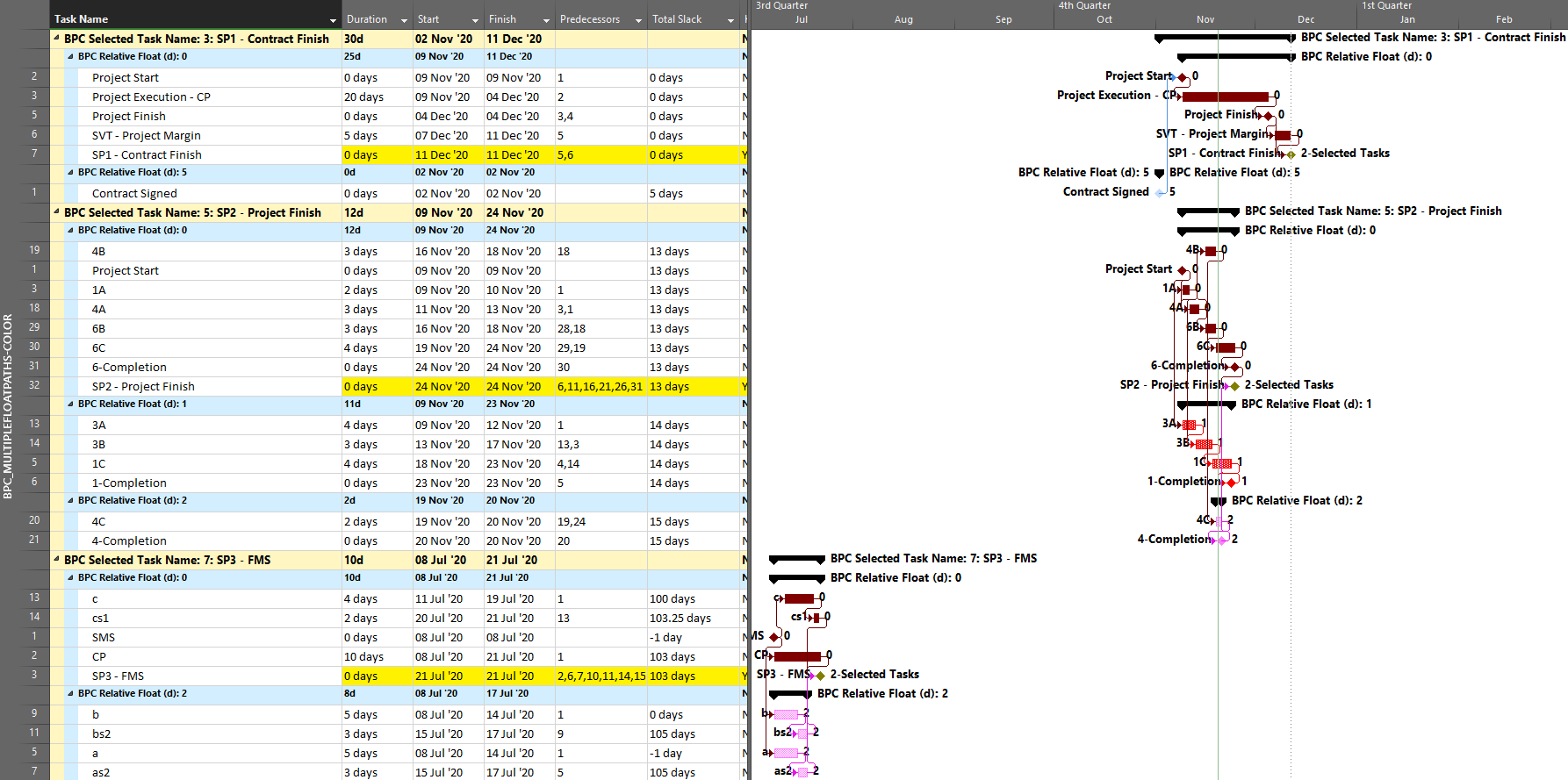
Updating the Project Schedule – Time Now and the Project Update Dialog in Microsoft Project
The absence of a dedicated time now or data date parameter in Microsoft Project makes regular schedule updates painfully difficult compared to other project scheduling software, but reliable and relatively quick updates are possible using the Project Update dialog.
Elements of Schedule Updates
Using modern project scheduling software, a schedule update that conforms to best-practices includes three key elements:
- Update Date/Time. Also called time now, the data date, status date, report date, or cutoff date. This date/time value represents the temporal boundary between the past and future elements of the schedule.
- (Past) Progress. I.e. historical documentation of actual activity dates, durations, work, costs, and sometimes physical completion. All reported progress occurs before the Update Date/Time; that is, in the past. Any non-actualized task dates (i.e. incomplete work) in the past are invalid.
- (Future) Forecast. I.e. remaining (not actualized) project work, costs, and activities that are uncompleted as of the update date/time and must therefore be executed in the future. Any actualized task dates (i.e. completed work) in the future are invalid.
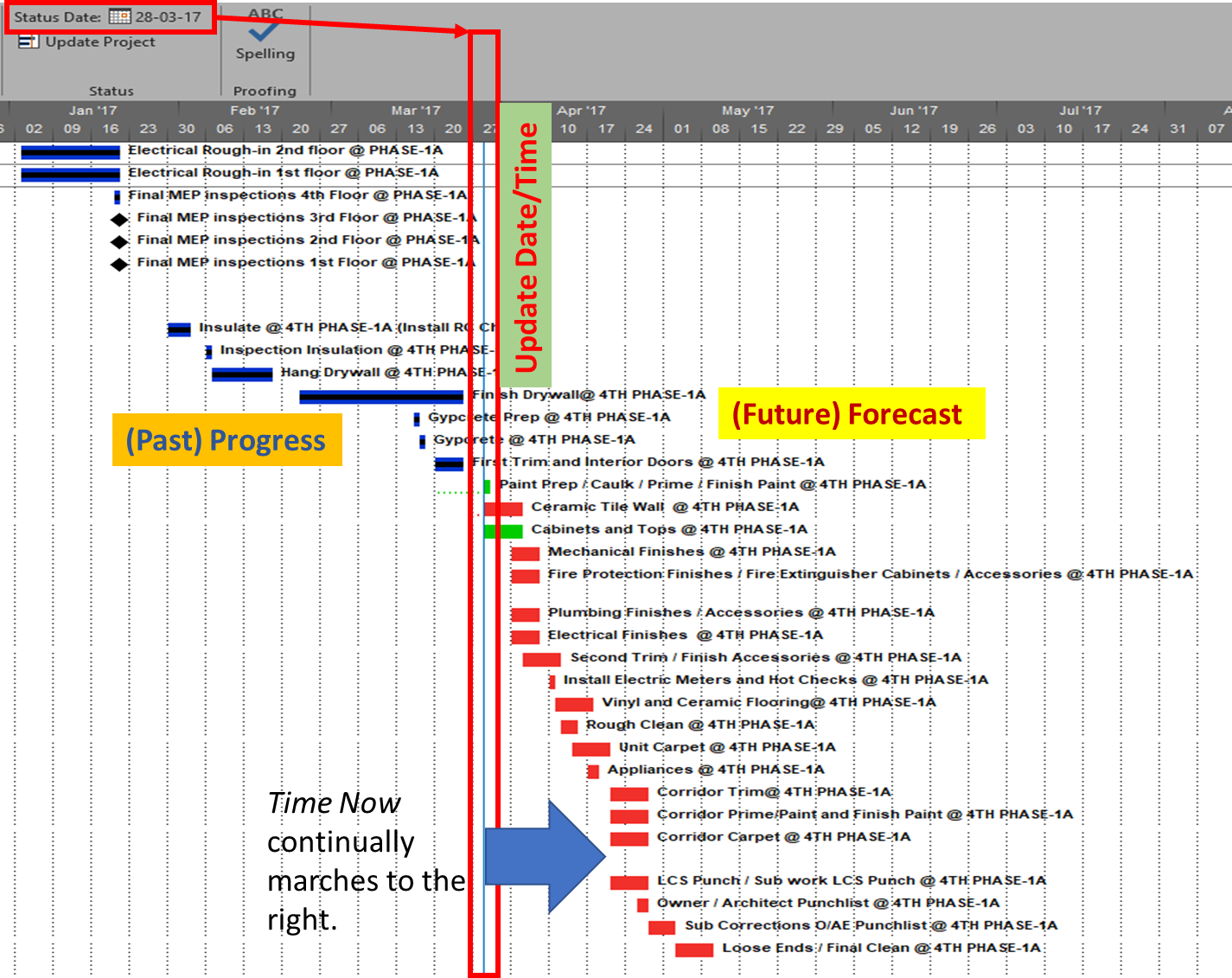
Generic Schedule Update Process
For a given update date/time, the past and future elements are defined through a two-step update process that endeavors to 1) update the status of each task to reflect the progress achieved (i.e. the completed work) as of the time now; and 2) update the overall status of the project by dynamically re-scheduling remaining work and forecasting the project completion in light of the current task status and sequential constraints. The forecast provided by this second step must encompass all remaining work, including any work that has slipped from previously-established dates and remains incomplete.
The first step of the process – task status updating – typically involves a mix of techniques leading to actual start dates, actual finish dates, and actual (and remaining) durations. In many projects, the accuracy of these actualized values is of only minor note, as the next step – re-scheduling the remaining work after time now – is considered far more important for day to day project management.
The second step of the update process – overall project status update (i.e. dynamic re-scheduling of remaining work) – is performed automatically by most schedule calculation algorithms. It typically requires nothing more from the user beyond resetting the time now date and clicking a function key.
Schedule Updates in Microsoft Project (MSP)
Unlike other modern project scheduling tools, MSP does not require any of the three elements named above, and the core updating functions seem focused on step 1, entering task progress (typically as duration %complete) against a static schedule. In fact, the well-developed options for configuring and displaying progress lines suggest a persistent reliance on such static-schedule updating methods among influential MSP users. [I first made progress lines about 35 years ago using paper bar charts hung on a corkboard, thumbtacks, and a weighted string. For a couple months I had the daily job of inserting a thumbtack on each bar to reflect the reported task progress at the end of the previous shift, then winding the string around the tacks to create the progress line. The line told everyone who was getting chewed out, but it said nothing about the current completion forecast or which work was most critical for the delivery. This static view of schedule progress made sense – for a week at a time in our version of pull-planning – back in the days when re-calculating a ship-construction schedule was much more labor intensive than clicking F9 is today.]
Task Status Updating
[Nov’20 Edit: I added this section after review with a colleague.]
MS Project provides a number of techniques for updating task status. I’ve listed the main ones here, generally in order of preference for project control…
- On a task-by-task basis, direct entry of actual dates, actual and remaining duration, and/or %Complete (which is definitely NOT preferred) in a user-customized task table, the default task Tracking Table, or the Task Details Form.
- For one or more selected tasks, direct entry of actual dates, actual and remaining duration, and/or %Complete using the Update Tasks dialog;
- For one or more selected tasks, clicking buttons on the Task ribbon with underlying wizards/scripts to enter a specific %Complete (0%, 25%, 50%, 75%, or 100%) or to Mark on Track (which automatically actualizes all progress as scheduled up to the project’s Status Date);
- For selected tasks or for all tasks in the project, using the upper portion of the Update Project dialog to “Update work as complete through:” any user-selected date. (This is essentially the same as Mark on Track, automatically actualizing all progress as scheduled up to the user-selected date, but defaulting to all tasks);
- For all tasks in the project, direct integration with timesheet entry systems (for actual start and actual work, on cloud-resident or server-resident projects only).
The program’s response to these inputs can vary widely, depending on overall program settings, individual task characteristics, and the order and timing of the entries. As a result, the methods for updating task status seem to vary widely between industries and even between competent professionals in the same industry. Some even use progress lines, though not for the same purpose I described earlier. The end objective is similar for all methods, however: the designation of specific tasks and parts of tasks as being completed (i.e. actualized), and therefore in the past.
Project Status Updating
The project status update first requires that all uncompleted tasks (and parts of tasks) are dynamically rescheduled to take place in the future. In a major difference from other tools, MSP does not directly incorporate a dedicated time now parameter in the schedule network calculations – like the data date in Oracle P6 and other software or the report date in Elecosoft Powerproject. Instead, the forward-pass calculations always begin at the project start, and the restraining effects of time now are achieved only by imposing external start-no-earlier-than (SNET) date constraints (for un-started tasks) or by delaying Resume dates (the start of the remaining duration for in-progress tasks.)
[Nov’20 Edit: I added the next paragraph after review with a colleague.]
In practice, some experienced MS Project schedulers explicitly effect these modifications on a task-by-task basis as part of the task status update above. Thus, when a task that should have had progress instead has none, the scheduler manually imposes a new SNET constraint either on the status date or on some other (later) promised date. Similarly, the actual and remaining durations of tasks with partial progress may be manipulated to straddle the status date. This manipulation can be done either manually or automatically, with the latter accomplished by entering task %Complete while the move start of… and move end of… advanced calculation options are enabled. (As a rule, however, any entry of task %Complete is normally to be avoided, and these advanced options can be more trouble than they are worth.)
MSP’s Update Project Dialog (2)
When the necessary constraints and Resume-delays on incomplete work are not imposed during individual task updating, the lower part of the Update Project dialog can be used on selected tasks. With “Reschedule uncompleted work to start after…”, the program compares the existing schedule Start/Resume dates for each task (in the selection or in the whole project, as indicated) to the update date that the user has specified. If the task’s Start/Resume date is a) not actualized and b) earlier than the specified date, then a SNET constraint or Resume-delay is imposed. (The latter action will be taken only if the schedule option for split-in-progress tasks is checked, the default setting.) The next time the schedule is re-calculated, the new constraints will be imposed on the early dates, thereby simulating the effects of an explicit time now.
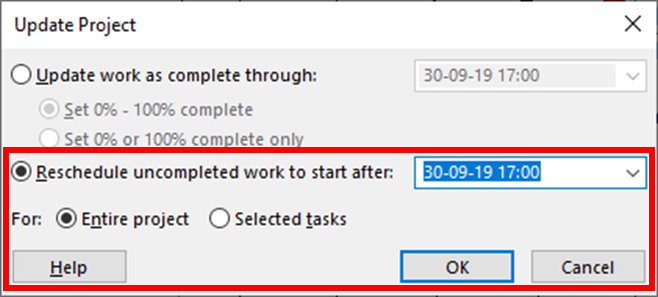
Issues with Update Project
- Although the Current Date or the project’s Status Date (if present) are pre-populated in the dialog, the Update Date is not limited. The user may choose any other date for re-scheduling any task or group of tasks. Thus, the schedule effect of a singular time now is susceptible to user interference, intended or not.
- Since MSP only allows the use of a single constraint for each task, the tool fails to re-schedule tasks with conflicting constraints. A SNET constraint with an earlier (non-conflicting) date will be replaced, but if a task with a late start, late finish, or early finish constraint is delayed, the new SNET constraint can’t be applied. The user must then either abandon the existing constraint or impose a delay using new synthetic logic.
- By default, the actions of the dialog are applied to the “Entire project,” and changing the option to “Selected tasks” only, if desired, must be repeated each time the dialog is opened. Using the default option with Reschedule uncompleted work to start after… typically imposes superfluous SNET constraints on tasks whose logical predecessors are similarly delayed.
- Since reliance on external date constraints is generally considered poor practice, the SNET constraints imposed during normal schedule updating in MSP may be flagged by schedule quality monitors. Users are tempted to evade such flags by introducing synthetic logic – especially on high-float tasks that are “riding the data date.”
- The numerous SNET constraints imposed through multiple schedule update periods need to be monitored and removed (after actualization) if the original project plan (i.e. logic and constraints) is to be maintained.
- Reschedule uncompleted work to start after… is not compatible with resource-leveled schedules. All resource leveling delays must be cleared before the tool is run, and the leveler should be called again only after the subsequent recalculation of the schedule network.
For a more comprehensive look at schedule updating in MSP, P6, and Elecosoft PowerProject, have a look at Paul Eastwood Harris’s detailed paper on the subject.
AACE International Annual Meeting 2020
Last month marked my second attendance at an Annual meeting of AACE International (formally Association for the Advancement of Cost Engineering). The Covid-19 Pandemic forced a change of venue from Chicago to Virtual/Online, with overall good results. Most of the technical presentations were pre-recorded for viewing at leisure. There was also a live track including keynotes, selected technical presentations, and business meetings. There were attempts to facilitate online “networking” and other informal “events”, but I missed those.
Earlier in the year, I co-authored a paper (with Patrick M. Kelly) for presentation at the meeting: (PS-3496) Interpreting Logic Paths in Multi-Calendar Project Schedules. It’s essentially a deep-dive into the Multiple Float Path calculation in Oracle Primavera P6 project scheduling software, expanding on (and in a few cases contradicting) my earlier blog articles, and Patrick’s paper, on the subject. A slightly revised version of the paper is hosted on our website. Pre-recording the presentation (as a narrated PowerPoint show) involved quite a bit more effort than a live presentation would have; I hope to become more efficient at it with additional practice.
The presentation (all 70+ minutes of it) and the paper are included in the Transactions bundle for registered attendees of the meeting. They are also available for purchase by non-attendees (including a training certificate after viewing the presentation) at the AACE store. I think the price is $25 for members of AACE and $30 for non-members.
I also got “elected” to the board of the Planning and Scheduling Subcommittee, and I look forward to taking over the coordination of our Recommended Practices from our rising Chairman, Jessica Colbert, for the next year.
Alternate Definitions of Driving Logic Relationships in Project Schedules
[Article 2 of 2.] This is a summary of the alternate definitions and uses of driving logic relationships between activities in project schedules, as applied in Primavera P6 and Microsoft Project software. Driving relationships are often considered fundamental elements of the project critical path.
This winter I worked with a colleague to prepare a paper – Interpreting Logic Paths in Multi-Calendar Project Schedules – for presentation at this year’s AACE International Conference and Expo in Chicago (Covid-19) virtual world. It’s a deep dive into the Multiple Float Path calculation options in Primavera P6 scheduling software. During the technical study, I had a lot of opportunities to think about driving logic relationships. I’ve summarized the standard definitions and uses in an earlier article. This entry summarizes the alternate versions of driving logic relationships that sometimes arise.
The Importance of Driving Logic
The planning and execution of complex projects requires the project team to understand, implement, and communicate the consequences of schedule logic flow to the other stakeholders. Through schedule logic, each activity in the project has the potential to constrain or disrupt numerous other activities – and to be constrained or disrupted by them. The most obvious artifacts of logic flow are the important logic paths, like the critical path, the Longest Path (in Primavera P6), or the driving path to a key delivery milestone. Regardless of the detailed definition, each of these important paths is governed by driving logic relationships from the first activity to the last activity in the path.
Late-Dates and Bi-Directional Driving Relationships in Primavera P6
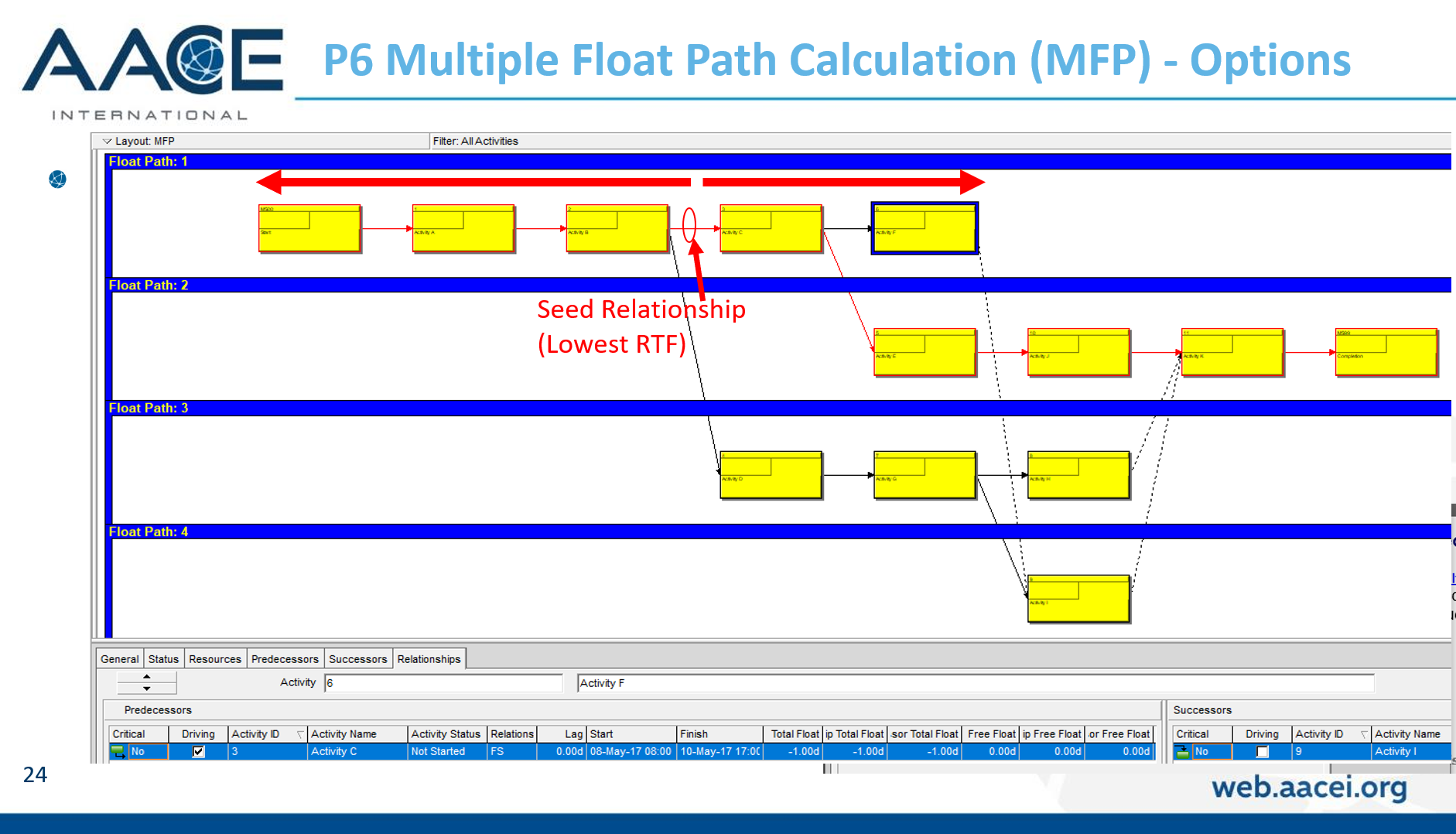
From the earlier article, a relationship is considered driving (under the standard definitions) when its successor’s early dates are constrained by the relationship, during the forward pass of the CPM calculations. That is, standard driving relationships are early-dates driving relationships. A late-dates driving relationship, in contrast, is one that constrains the late dates of the predecessor, during the backward pass. When an activity has multiple successors, then one or more of these successor relationships may be controlling the late dates, and hence the total float, of the selected activity; this is a late-dates driving relationship.
Identification of late-dates driving relationships is a key factor in P6’s Multiple Float Path (MFP) calculation. Under the total float calculation option, a relationship can be assigned to a driving “float path” only if it meets the criteria for both early-dates and late-dates driving relationships. That is, it possesses bi-directional driving logic. Since P6 does not flag or otherwise mark such relationships, the results of multiple float path calculations with the total float option can be confusing. Full understanding of the float paths may require a detailed examination of relationship and activity floats, especially when multiple calendars or constraints are involved.
For more information on MFP calculations in P6, check out these other entries in the blog:
Beyond the Critical Path – the Need for Logic Analysis of Project Schedules
P6 Multiple Float Path Analysis – Why Use Free Float Option
Relationship Free Float and Float Paths in Multi-Calendar Projects (P6 MFP Free Float Option)
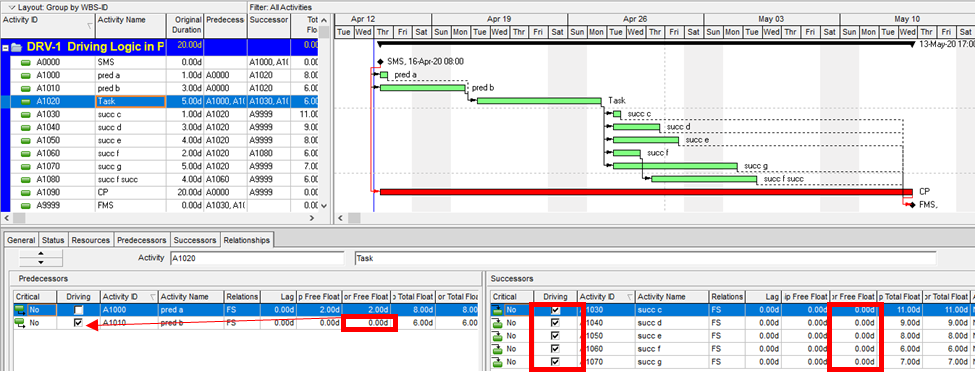
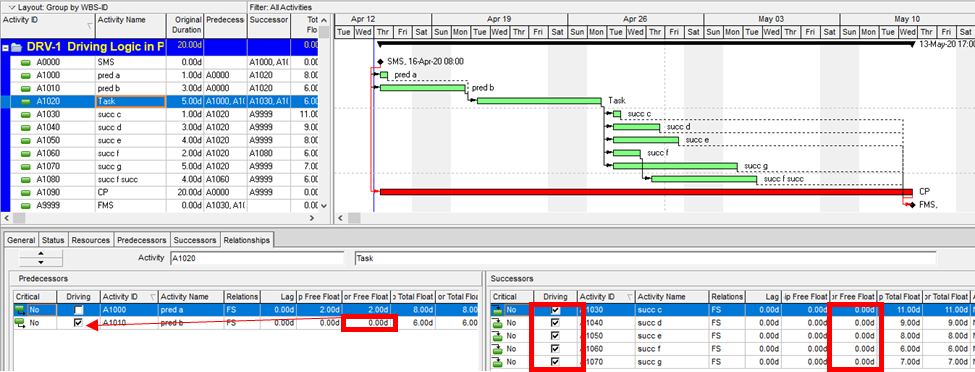
Aside from the MFP calculation option in P6, this type of driving logic is useful mainly for prioritizing driving successors when click-tracing through the schedule network in the forward direction – perhaps for schedule validation or disruption analysis. For example, consider the selected activity (A1020, “Task”) in the P6 version of our simple project below. A glance at the late-date bars shows that only one of its five driven successors (A1060, “succ f”) is responsible for the late dates (and total float) of the selected task. The corresponding relationship possesses bi-directional driving logic and marks the forward continuation of the total-float-based driving path. In the relationship tables, the “Driving” checkboxes already indicate the relationships with early-dates driving logic. When exploring forward, most P6 users will simply click to the driven successor activity that is “Critical” or has the lowest total float value, and that will be correct much of the time. When multiple constraints and/or calendars exist, however – or when the path being explored is far from critical – then late-dates driving logic is indicated when the “Relationship Total Float” equals the total float of the predecessor activity, as highlighted in the figure.
Late-Dates and Bi-Directional Driving Relationships in BPC Logic Filter
With no built-in alternatives, BPC Logic Filter automatically identify all three types of driving relationships – early-dates, late-dates, and bi-directional – in Microsoft Project schedules. The next figure repeats the same simple example project from the earlier article, with additional bars for early and late dates (green and red) and the task paths shown earlier (orange, gold, purple.) Within the logic inspector tables, bi-directional driving relationships are highlighted (red/yellow) and shown on top. Among those relationships that are NOT bi-directional drivers, early-date drivers are shown in the same yellow as before, and late-date drivers are shown in pale red. As usual, the logic inspector’s jump buttons make for easy, logic-based navigation through the schedule.
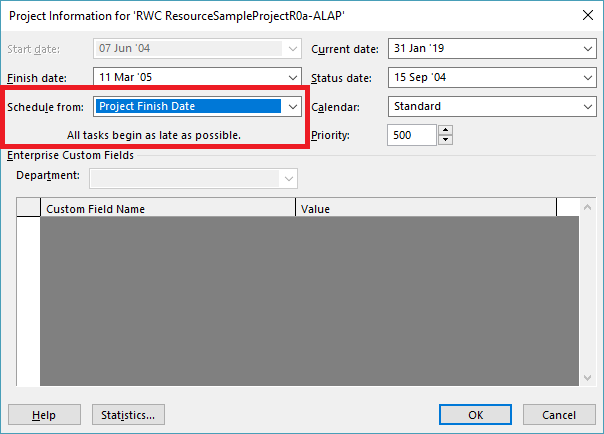
Unlike MSP’s built-in task path bar styles, the logic inspector tables are equally effective at illustrating driving logic in backward-scheduled projects. This is demonstrated below, where the same example project has been re-configured to Schedule from: Project Finish Date. Interestingly, while the scheduled dates clearly change, the nature of driving logic relationships does not.
For further information on driving logic in backward-scheduled projects, check out this earlier entry: Driving Logic in Backward Scheduled Projects (Microsoft Project), which pre-dated the introduction of late-dates driving calculations in the logic inspector.
Resource Driving Logic Relationships in BPC Logic Filter
When resource leveling is imposed in a P6 or MSP project schedule, some tasks are delayed from their CPM-based early dates until resources become available – after completion of other tasks. In the figure below, a single resource has been assigned to the five successors of the “Task,” and the resulting overallocation of the resource has been resolved by leveling the schedule using the simplest options. As a result, the project finish milestone has been delayed by three days, and the critical path has shifted.
The leveling process creates implied driving relationships between tasks that demand the same resources. BPC Logic Filter infers these “ResDrvr” relationships. As shown below, the resulting resource-constrained driving logic paths are typically very different from those identified using CPM logic alone.
The consequences of resource driving logic are further addressed in these earlier articles:
The Resource Critical Path – Logic Analysis of Resource-Leveled Schedules (MS Project), Part 2
Hierarchical (Parent-Child) Driving Logic Relationships in Microsoft Project
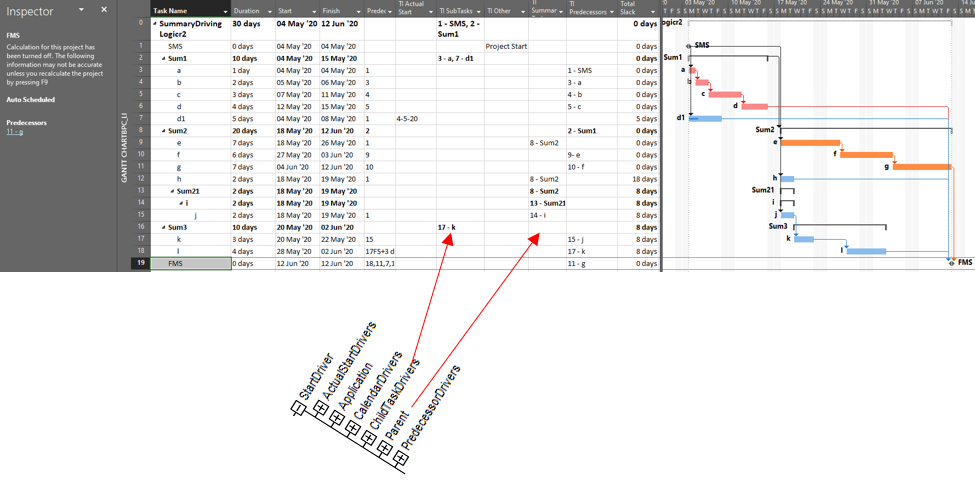
Unlike other project scheduling tools, MSP supports direct assignment of schedule logic (start predecessors and finish successors only) to “summary tasks.” As a consequence, it then imposes automatic logic restraints based on the relative positions of tasks within the Outline/Work breakdown structure. Thus, a summary task with a finish-to-start predecessor automatically imposes a corresponding early-start restraint on every one of its subtasks, and this restraint is inherited at each outline level all the way to the lowest-level subtask. Moreover, a summary task with a finish to start successor automatically imposes a corresponding late-finish (backward-pass) restraint on its subtasks, which is inherited all the way down the outline structure. External date constraints, manual-mode scheduled dates, and actual dates inputs for summary tasks have similar consequences.
The immediate early-start drivers for summary tasks and subtasks – whether a result of predecessor logic, outline-parent inheritance, or outline-child roll-up – can be identified by the task Inspector as shown in the next figure, and some of these are explicitly enumerated in the “driver” collections of the task. The late-date consequences remain implicit, however.
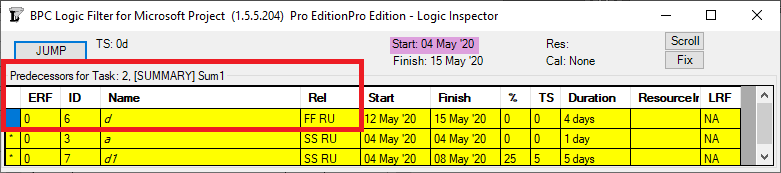
The apparent critical path for the schedule of the previous figure runs through tasks a-d and tasks e-g, including their driving FS relationships. Not shown, however, is the implicit driving FF relationship from task d to its outline parent task Sum1 (here identified in BPC’s logic inspector tool.)
The implicit driving SS relationship from task Sum2 to its outline child task e is correctly identified by the task inspector as well as BPC’s logic inspector.
Those two implicit hierarchical relationships – when combined with the explicit Sum1-to-Sum2 FS relationship – are necessary to properly calculate early and late dates and total slack, which is the source of the critical path depicted. Unfortunately, the built-in tools are not sufficient to fully trace driving logic through such hierarchical relationships, even in this simple schedule.
Neither summary-task relationships nor the consequent hierarchical (parent/child – child/parent) relationships are explicitly recognized in the generally accepted, traditional understandings of logic-based project scheduling – i.e. the critical path method (CPM) and the precedence diagramming method (PDM). Such relationships are not generally supported in other scheduling tools, either, so attempts to migrate MSP schedules containing summary logic into other tools for analysis are typically unsuccessful. It is also clear that adding even a small number of summary-task relationships to a moderately complex project schedule can potentially obfuscate the driving logic paths in the schedule, including the critical path under many circumstances, without fairly sophisticated analysis. Taking these facts together, most project scheduling professionals seem to agree that summary-task logic in MSP represents poor practice and is to be avoided.
Driving Logic Relationships in Project Schedules
[Article 1 of 2.] This is a summary of the standard definitions and uses of driving logic relationships between activities in project schedules, as applied in Primavera P6 and Microsoft Project software. Driving relationships are often considered fundamental elements of the project critical path.
This winter I worked with a colleague to prepare a paper – Interpreting Logic Paths in Multi-Calendar Project Schedules – for presentation at this year’s AACE International Conference and Expo in Chicago (Covid-19) virtual world. The paper reflects a deep dive into the Multiple Float Path calculation options in Primavera P6 scheduling software. During the technical study, I had a lot of opportunities to think about driving logic relationships. This entry summarizes the standard definitions and uses. I’ve summarized a couple alternate definitions and uses in another article.
The Importance of Driving Logic
The planning and execution of complex projects requires the project team to understand, implement, and communicate the consequences of schedule logic flow to the other stakeholders. Through schedule logic, each activity in the project has the potential to constrain or disrupt numerous other activities – and to be constrained or disrupted by them. The most obvious artifacts of logic flow are the important logic paths, like the critical path, the Longest Path (in Primavera P6), or the driving path to a key delivery milestone. Regardless of the detailed definition, each of these important paths is governed by driving logic relationships from the first activity to the last activity in the path.
Standard Definition and Uses of Driving Logic Relationships
A driving relationship is “A relationship between two activities in which the start or completion of the predecessor activity determines the early dates for the successor activity with multiple predecessors. See also: Free Float.” [That’s the standard definition from AACE International.] Alternately, “A driving relationship is one that controls the start or finish of a successor activity.” [That’s from the PMI publication on CPM Scheduling for Construction.]
For practical purposes, a driving relationship is a predecessor relationship that prevents a successor activity’s early start or early finish from being scheduled any earlier than it is. When an otherwise unconstrained activity has only one predecessor, then it is normally, and obviously, a driving predecessor. When an activity has multiple predecessors, then one or more of them may be driving while the others are non-driving. These distinctions answer the key questions, “Why is this activity scheduled when it is? Why can’t we do it sooner?”
Driving Logic in Primavera P6
Like its predecessors, P6 routinely illustrates driving logic relationships using solid lines on bar charts – either red or black depending on the “Critical” status of the connected activities. Non-driving relationships are depicted with the same colors, and those that are also non-critical use dotted lines. This is demonstrated in the figure below, where the non-critical activity “Task” (A1020) has two predecessors and five successors. One of the predecessor relationships and all five of the successor relationships are depicted with solid black lines and marked as driving (but not critical) in the relationship tables. The non-driving relationships – one from “pred a” to “Task” and five more from Task’s successors to the project’s finish milestone – are depicted with dotted lines. The two critical, driving relationships that connect the “CP” activity to the project’s start and finish milestones are depicted with solid red lines.
In small projects it is often easy to identify driving logic flow in printed P6 bar charts by visually tracing the solid relationship lines between activities. As project schedules become larger and more complex, however, the number of relationship lines increases to the point that visual tracing becomes impractical. Then driving relationships are primarily identified using the relevant columns of the associated relationship tables. Experienced P6 users often use the “GoTo” buttons in the relationship tables to click-trace along driving logic paths – backward and forward through complex project schedules – to review and confirm important chains of sequential logic (i.e. driving logic paths).
In general, Primavera P6 identifies driving relationships by analyzing the intervals between early dates of the linked activities, after completion of the core scheduling calculations. With a few minor exceptions, a driving relationship is identified when the Relationship Successor Free Float (RSFF) equals zero. In addition to providing a basis for the graphical and tabular depictions of driving logic flow, P6 uses these driving attributes to automatically identify the Longest Path, or the driving path to project completion.
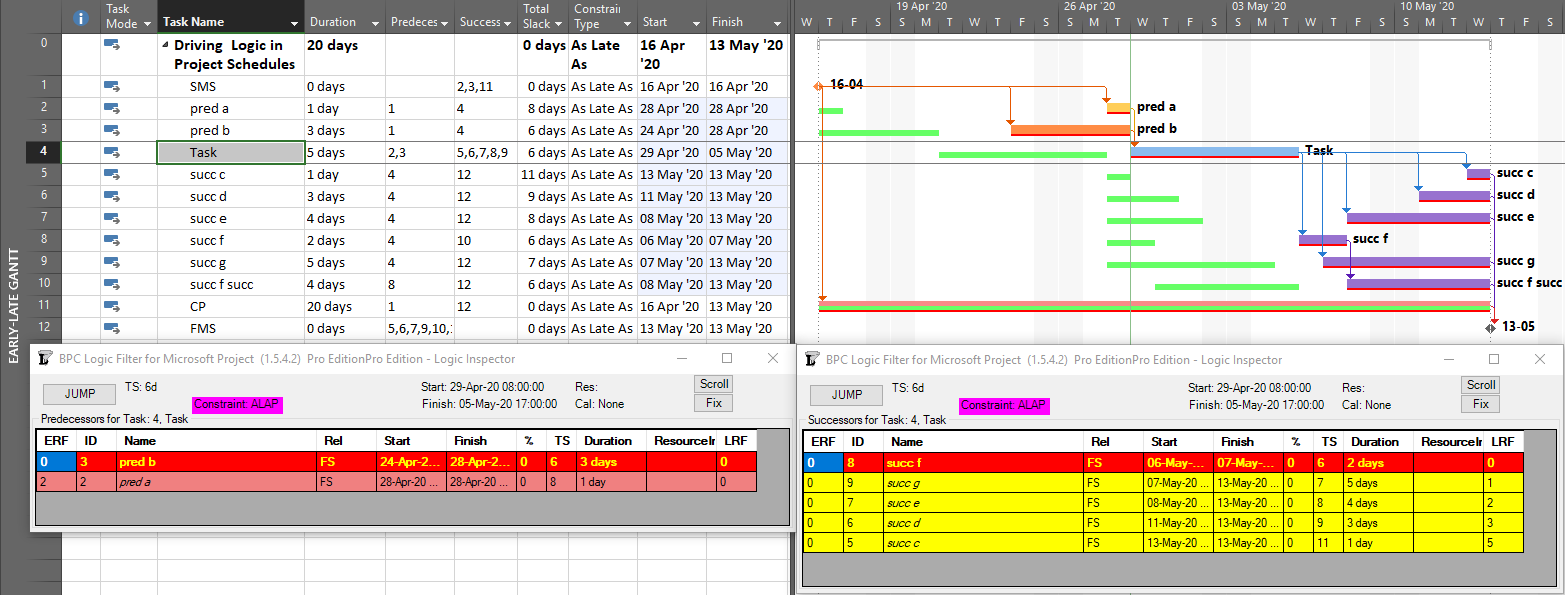
Driving Logic in Microsoft Project
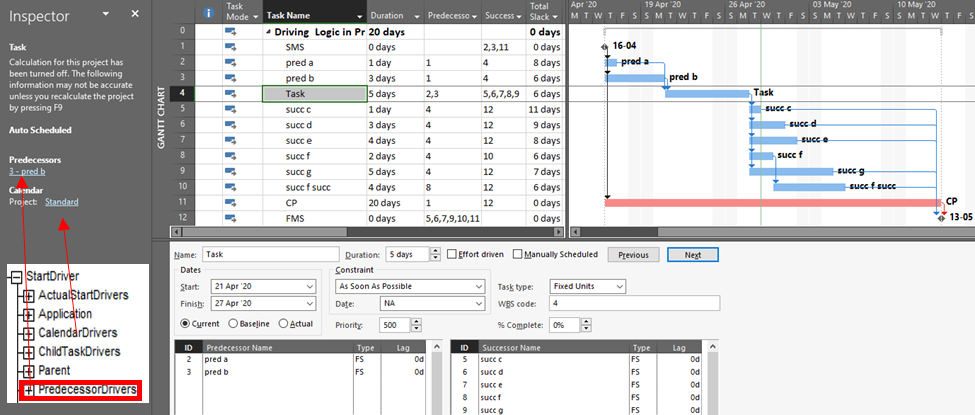
Unlike P6, Microsoft Project (MSP) does not graphically differentiate driving and non-driving relationship lines in Gantt-chart views, and the standard relationship (i.e. dependency) tables provide no driving-logic indicators. The Task Inspector pane provides the primary method for identifying driving predecessors of the currently-selected task; there is no corresponding method for identifying driven successors. The figure below depicts the same schedule as before, now in MSP format, with the Inspector pane identifying a single (driving) predecessor task, “pred b”, for the currently-selected task (“Task.”) As far as it goes, this agrees with P6.
Although not presented to users, driving relationship indicators are developed by MSP (at least since MSP 2007), with the results being stored in the PredecessorDrivers collection for each task. This collection forms the basis of the Predecessors list of the Inspector pane.
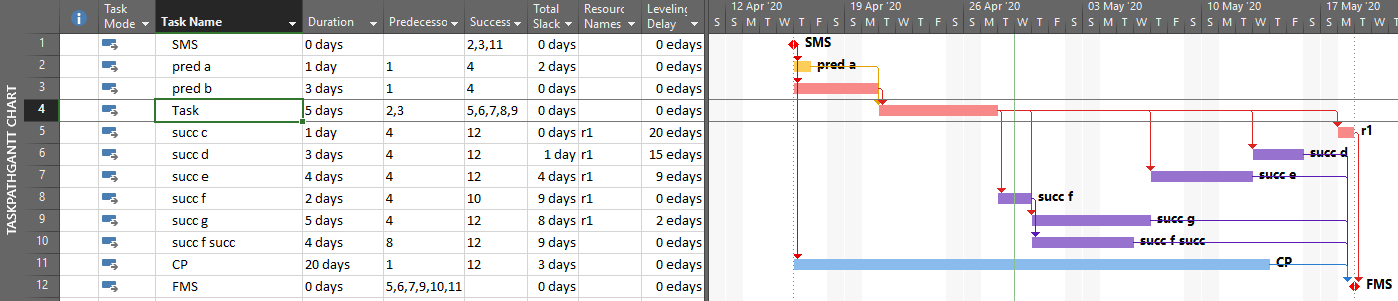
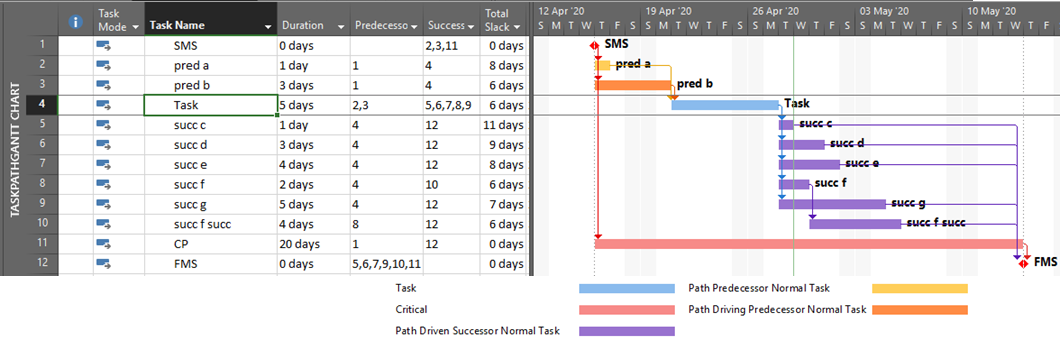
It’s also apparent that the PredecessorDrivers data are used to define the Driving Predecessors and Driven Successors bar styles that were introduced as part of the Task Path functionality in MSP 2013. This functionality is illustrated below, where the driving and non-driving predecessors of “Task” – and its driven successors – are all differentiated by bar color. Although there are clear limitations to this graphical approach, the ability to show driving and driven logic paths (if not individual driving relationships) is a major improvement for MSP users.
Unfortunately, the internal MSP calculation of driving logic attributes – and the explicit paths of driving logic that they purport to illustrate – have proven unreliable for complex schedules with other than finish-to-start relationships, out-of-sequence progress, or external links.
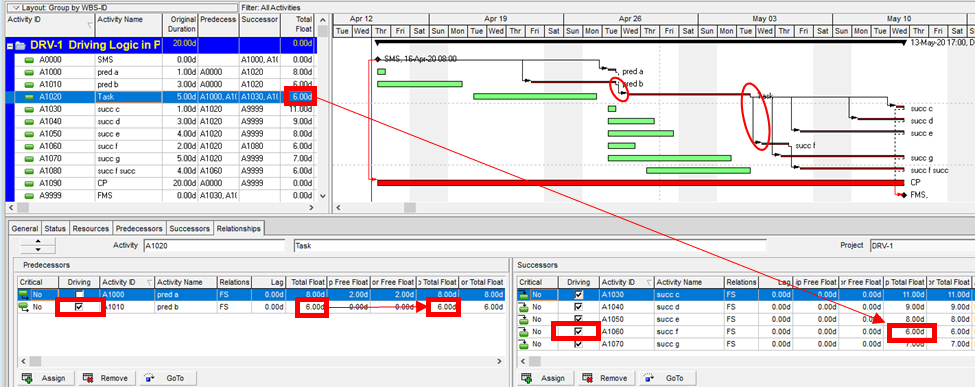
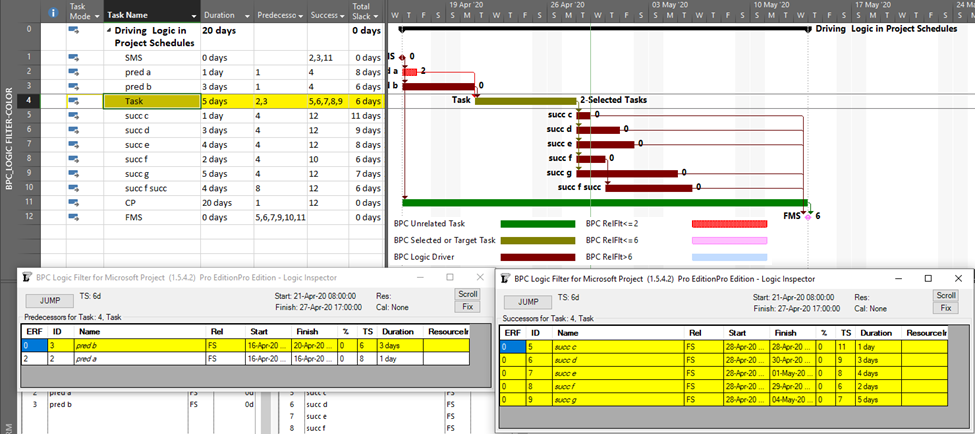
Standard Driving Logic in BPC Logic Filter for Microsoft Project
BPC Logic Filter (my company’s add-in for MSP) identifies driving logic by independently analyzing relationship relative floats after completion of the schedule calculations. This is a bit like the P6 approach and has proven, at least for me, more reliable than the internal MSP data when things get complicated. This figure shows the combination of a logic tracer view (with special bar styles depicting driving and near-driving logic paths) together with the task logic inspector tables. Driving relationships are highlighted yellow in the tables. Overall, this seems to combine the best parts of the corresponding P6 and MSP layouts, and the Jump buttons allow for logic-based navigation forward or backward through the schedule network.
Continue to related article…
Alternate Definitions of Driving Logic Relationships in Project Schedules
Construction CPM Conference 2020 – Avoid Out of Sequence Progress in Microsoft Project
Click Here to view the screen and audio capture of my presentation at the 2020 Construction CPM Conference. Fred Plotnick (the Conference organizer) is kind enough to host the content on his server.
The presentation recaps and expands on my blog entry on the same subject: Avoid Out-of-Sequence Progress in Microsoft Project 2010-2016.
Construction CPM Conference 2019 – Schedule Logic in Microsoft Project
Click Here to view the screen and audio capture of my presentation (on BPC Logic Filter) at the 2019 Construction CPM Conference. Fred Plotnick (the Conference organizer) is kind enough to host the content on his server.
Most of this will be familiar to those who’ve already seen one of my presentations on BPC Logic Filter, but the questions and answers beginning at about minute 59:00 are new.
Driving Logic in Backward Scheduled Projects (Microsoft Project)
Microsoft Project’s backward scheduling mode includes numerous traps for novices and professionals alike. Competent project schedulers avoid it.
In MSP, a backward scheduling mode – sometimes called backward planning, reverse scheduling, or reverse planning – can be invoked by scheduling the project from its finish rather than its start. In the traditional language of critical path method (CPM) scheduling, it’s most simply described as a late-dates schedule. Backward planning is useful in several non-standard methodologies, including critical chain project management and the pull planning aspects of the Last Planner System.
The Mechanics of Backward Scheduling
When specified for the active project, this mode essentially does the following:
- Sets the default constraint type for all new tasks to as late as possible (ALAP).
- Re-sets the constraint type to ALAP for all existing Summary tasks.
- [Users choosing this mode in the middle of schedule development must manually re-set the constraint type to ALAP for all existing non-Summary tasks.]
- Automatically sets no later than constraints when dates are manually entered into the start or finish fields of tasks. [Such date entry in forward scheduling mode leads to “no earlier than” constraints, so users choosing this mode in the middle of schedule development should manually review, validate, and potentially re-set any previously-entered date constraints.]
- Performs the network scheduling calculations in reverse order, with the reflection point occurring at the project start rather than the project finish. I.e. the project start date (not the finish, which is user-input) is determined by the logic.
- Sets the start and finish of automatically-scheduled tasks to their late dates rather than their early dates. (This is the most important part.)
- Finally, the resource leveling engine resolves resource over-allocations by accelerating higher priority tasks from late dates rather than delaying lower priority tasks from early dates. Thus, entries in the leveling delay field are negative. This behavior creates a minor complication regarding use of priority = 1000. Just as in forward scheduling, a task with priority=1000 is always exempted from any leveling action. In backward scheduling, this means that priority values of 1000 and 0 are essentially equivalent when considered in the leveling decisions. The highest effective priority for controlling leveling behavior then becomes 999, not 1000.
Logic relationships used in backward scheduling still have exactly the same meanings that they do in forward scheduling. A finish-to-start (FS) relationship still means that the two tasks are logically connected such that the successor may not start before the predecessor finishes, and the rarely-applicable start-to-finish (SF) relationship still indicates that it is impossible for the successor to finish before the predecessor starts. Some users seem to think that backward scheduling involves reversal of these two relationships in particular, but that’s not consistent with the rest of the backward scheduling mode. Unfortunately, mixing of the two approaches seems to continue, though this typically amounts to invalid date manipulation in my view.
In normal (i.e. forward) scheduling, a task with an ALAP constraint has the dubious distinction of corrupting its entire chain of successors – driving all of them to the critical path. There are very few legitimate applications for this constraint. In backward scheduling, the as soon as possible (ASAP) constraint plays a similar role, corrupting its chain of predecessors. It needs to be avoided in backward scheduling.
When to Use Backward Scheduling
I’ve never used backward scheduling in a real project. Others have recommended its use to determine the desired start date of a project when the desired completion date is already known. It also seems consistent, when tasks are suitably buffered, with aspects of critical chain project management that require work to be scheduled as late as possible.
Ultimately, backward scheduling rests on the presumption that tasks can be accelerated (i.e. moved to the left on the bar chart) indefinitely as needed to meet the fixed end date for the project. Thus, a task whose duration is extended can simply be re-scheduled to start sooner than previously planned, with its predecessors also being accelerated. Similarly, a higher priority task can be started (and finished) earlier to avoid resource conflicts with a lower-priority task that demands the same resources. The problem with these presumptions is that time invariably marches forward, and as scheduled dates for incomplete work are overtaken by the vertical time-now line on the bar chart there is no chance for recovery. The backward scheduling method is pointless if the latest allowable project start date has already been passed – e.g. the project is in progress.
Backward scheduling seems to be of primary value in determining the latest responsible date to start a project (or project segment) while still meeting the desired completion date. After that latest responsible start date is determined, the project must be converted from backward-scheduled to forward-scheduled mode – manually reviewing and revising the key parameters of each task – if it is to be used for updating and forecasting during project execution. The original question – i.e. what is the latest responsible project start date? – is just as easily answered by manipulating and examining the late dates of the forward scheduled project. Thus, for a competent project scheduler, the use of backward scheduling seems largely to be an unproductive diversion.
Driving Logic Analysis
When the logic network is well constructed – and complicating factors like multiple calendars, (early) constraints, and resource leveling are avoided – then the critical path may be reasonably identified by total slack = 0. Other methods of driving logic analysis must be modified, however.
Under backward scheduling, any slack/float of a task exists on the side towards its predecessors, i.e. to its left on a bar chart. A driving relationship exists when a successor prevents a predecessor from being scheduled any later than it is. This means that there are driving successors and driven predecessors. Consequently, the Longest Path in a backward scheduled project is the driving (successor) path from the project’s start.
MSP includes two built-in methods for reviewing and analyzing driving logic: the Task Inspector pane and the task paths bar styles. As I wrote in this article a few years ago, I’ve found these tools to be unreliable in complex real-world project schedules. Under backward scheduling, they are essentially useless and/or misleading.
To start with, Task Inspector simply doesn’t work with backward scheduling. Opening TI on a backward scheduled project yields the following message: This project is set to Schedule from Finish. We are unable to provide scheduling information.
Also under backward scheduling, the Driving Predecessors and Driven Successors bar styles are still derived from Early Dates, as they are in Forward Scheduling. This makes them essentially useless for assessing the controlling logic of the displayed (late-dates) schedule. Consider the example below, where all four Task Path bar styles have been imposed, and Task 11 – A2 Structures – is selected. (The automatic “Slack” bar style is also imposed, but it is invisible since Free Slack – formally defined by Early dates alone – is uniformly zero.) 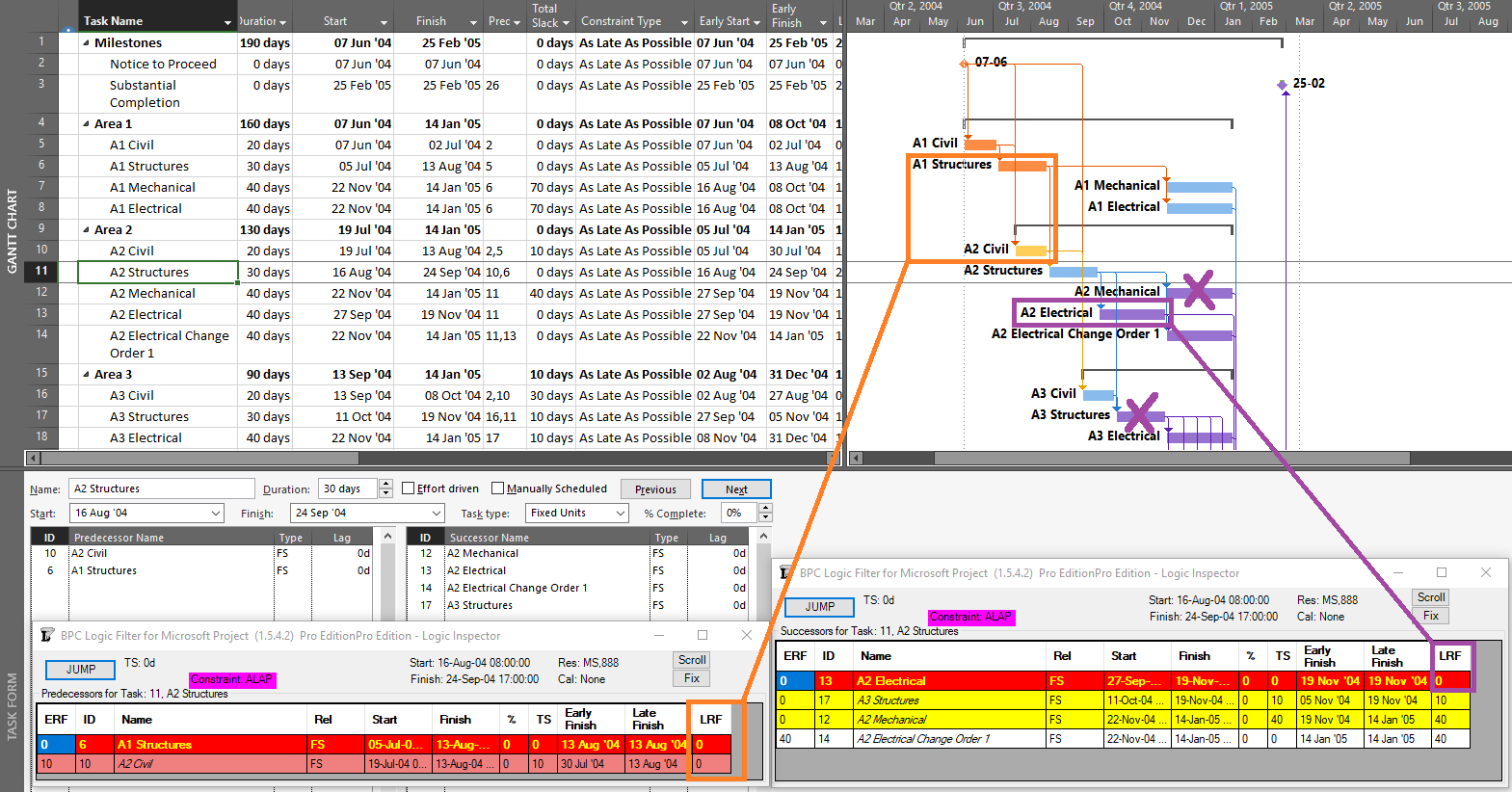
The selected task is in fact driving/controlling the displayed dates of both of its predecessors (LRF=0), but only one of them displays the correct bar style (the one that, with ERF=0, was the driving predecessor during the forward pass). Of Task 11’s four successors, only the first (Task 13 – A2 Electrical) is directly driving/controlling Task 11’s schedule, with LRF=0. The tasks for two of the remaining three successor relationships are incorrectly highlighted, while the third (Task 14) is correctly highlighted only because it is driving/controlling Task 13 – a case of redundant logic. (All four successors were driven successors during the forward pass.) Thus in a backward scheduled project, the Task Path bar styles for Driving and Driven dependencies are meaningful (or “correct”) ONLY along the Longest/Critical path of the project, where Early dates and Late dates coincide. The relationships along that path are driving in both directions; i.e. they are bi-directional driving relationships.
BPC Logic Filter – my company’s Add-In for logic analysis of MSP schedules – identifies driving logic based on relationship free float, which we often call “relative float.” In BPC Logic Filter, the Longest Path and near-longest paths of simple, backward-scheduled projects can be found using the Task Logic Tracer, starting from the project start milestone and using appropriate settings (i.e. driving relationships in successor direction). As illustrated in the example project, this is fairly trivial since the results are 100% aligned with Total Slack. 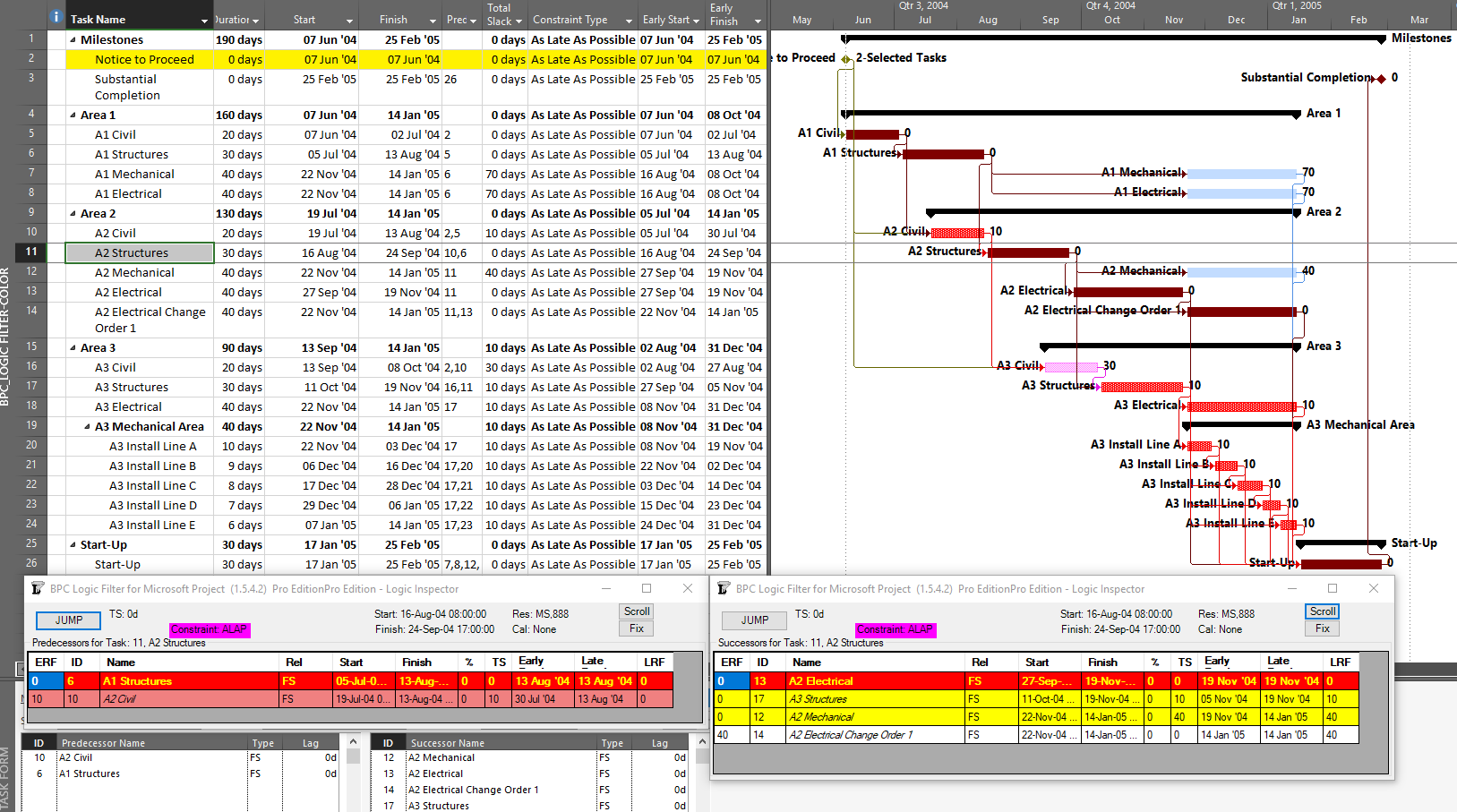
Other driving logic paths (not on the Critical Path) are not so trivial but are easily addressed using BPC Logic Filter, provided that the impact of multiple calendars is minimal.
Precision analysis of more complex, backward-scheduled projects requires some modest modifications to the algorithms. In particular, several variations of late-relationship-float need to be computed, and these have been added to the development roadmap for the software.
[Apr’20 Revision. I’ve updated the two figures to incorporate the early-date relative float (ERF) and late-date relative float (LRF) columns in the logic inspector windows. Calculation of the latter was only added to recent builds of BPC Logic Filter. These windows also flag the forward-driving (yellow), backward-driving (rose), and bi-directional-driving (red/yellow) relationships.]
BPC Logic Filter – Version 1.5 Improvements
The latest release of BPC Logic Filter – an Add-in for schedule logic analysis in Microsoft Project – includes direct implementation of the QuickTrace macros, faster logic-related formatting of Gantt chart bars, additional controls for logic-based schedule navigation, and overall snappier performance.
Introduction
My company started sharing BPC Logic Filter, our Add-in for Microsoft Project, in 2015. Since then, we’ve made incremental improvements to the tool that get shared in real time. Many of these improvements were prompted by informal user feedback, for which we are most grateful. Version 1.5, released in January 2019, brings a few nice little goodies that we’ve been anticipating for a while….
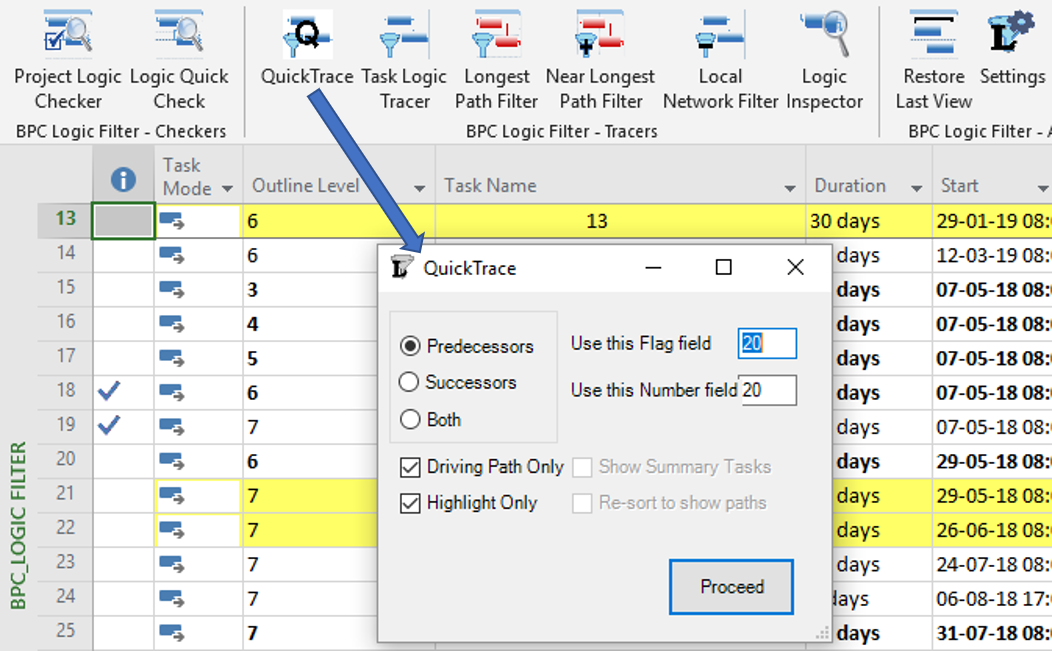
QuickTrace
QuickTrace is a set of macros for simplified logic tracing and filtering in MSP. I wrote the original macros for a blog entry several years ago, and subsequent high traffic on that entry implies that a fair number of MSP users are downloading and implementing the macros. We’ve now partially integrated that code with the rest of the add-in, providing a new ribbon button and a dedicated form, and including QuickTrace in the daily logs.
Eventually, we may get rid of the two boxes for selecting custom fields, streamlining the form even more.
QuickTrace is fully aligned with MSP’s internal “Task Inspector” and the associated “Task Path” bar styles (in MSP 2013+). Like the two native tools, QuickTrace relies on internal MSP calculations for identifying “driving” logic. This makes it blazing fast compared to the rest of BPC Logic Filter. Also like the two native tools, it incorrectly identifies driving logic paths in the presence of certain (fairly common) complicating factors.
We’ve included QuickTrace as a reasonable accessory. It is particularly useful when there is a need to compare its results with those of the other logic Tracers in BPC Logic Filter. (This is the chief argument for leaving the QuickTrace custom fields as user-selected, outside the Add-in’s normal routines for selecting and managing its use of custom fields.)
[Because it relies on recursion (a kind of repeated “cloning” of itself), QuickTrace is subject to memory-overload errors. This restricts the maximum path length that can be evaluated before “crashing out.” Based on limited testing, the memory-limited maximum path length (in number of tasks) varies by MSP version and execution environment, as summarized here (figures are approximate).
The two obvious conclusions from the table are: 1) MSP 2016 imposes a much larger memory burden than MSP 2010, especially in the nominally-internal vba environment. 2) Compared to the macro/vba, BPC Logic Filter’s implementation of Quicktrace is far less likely to run out of memory on a very large project. This advantage is amplified in MSP 2016. On the downside, the out-of-memory add-in will crash hard, taking your data with it, while the macro/vba solution tends to crash softly.
For the add-in, QuickTrace’s lowest path-length limit – at 7,740 tasks – corresponds to 30 years of 1-day tasks arranged finish-to-start. It seems unlikely that this limit could be reached in a real-world project of at least moderate complexity. Nevertheless, as always, save early and save often.]
Bar Formatting Improvements
The first major upgrade of the tool (v1.1) included the ability to add certain logic-related information to bars in a Gantt Chart, specifically by modifying bar shapes, colors, and text. Such information would be particularly useful for displaying related tasks within the context of an unfiltered view of the overall project schedule (i.e. “In-Line Only”), though I’ve had the habit of re-coloring bars in virtually all analyses.
For several reasons, bar coloring can impose a substantial time penalty on the completion of a logic analysis in BPC Logic Filter, with the size of the penalty being proportional to the number of tasks ultimately displayed. Recent releases of Microsoft Project (e.g. MSP 2013+) have increased the size of this penalty while also introducing some erroneous coloring results for in-progress tasks. Consequently, coloring Gantt bars in very large projects typically has been something to avoid.
Accelerated Bar Coloring
The new “Accelerate Bar Coloring” option is implemented via a single checkbox in the Bar Preferences tab – accessed directly through the “Settings” button on the Ribbon or indirectly through the “Bar Chart Options” button on the control window for each Tracer.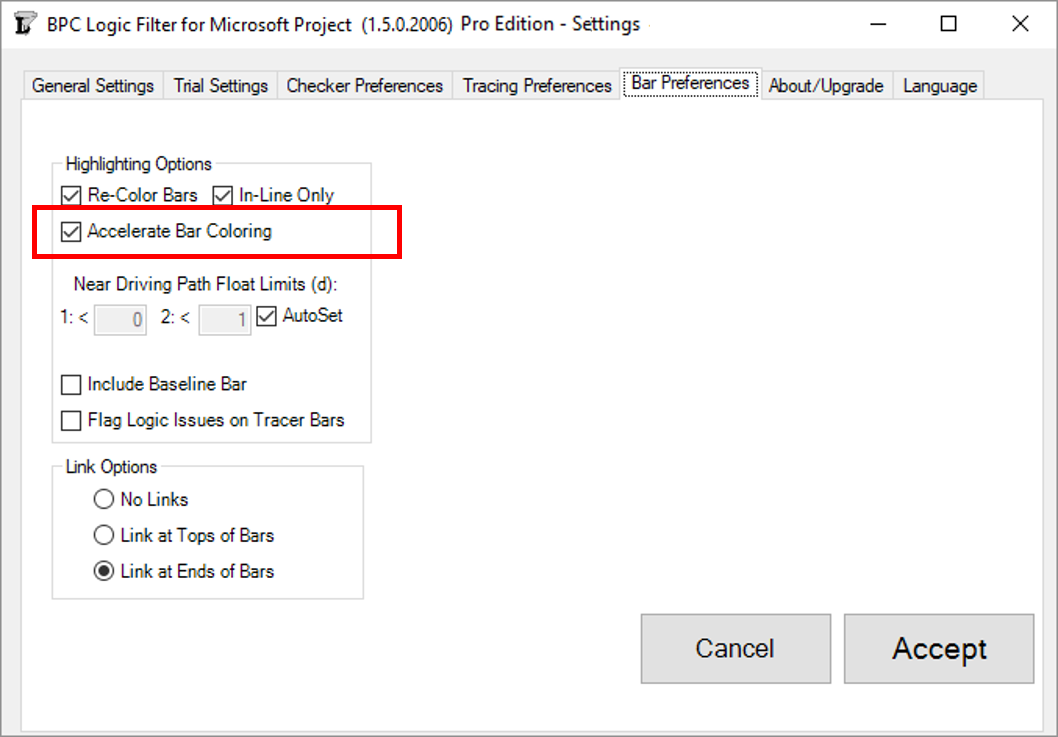
This option introduces an alternate bar coloring process that:
- Draws bars more quickly for large filter outputs, with the largest outputs seeing the greatest gain. For example, I have configured a Near-Longest-Path analysis of an 18,000-task schedule to include every task in the output filter. Without bar coloring, the overall analysis takes just under two and a half minutes (145 seconds) on my laptop computer. With Accelerated Bar Coloring, the overall analysis takes 13 seconds more (158 seconds). With traditional bar coloring, the overall analysis takes nearly 20 minutes more!
- Overcomes issues of incorrect bar coloring for in-progress tasks (MSP2013+).
- Constructs and manages up to 25 new bar styles for uniquely and accurately describing the output. In contrast to the other option, these bar styles can be readily modified and augmented by advanced users of MSP.
These improvements can make the coloring of Gantt bars no longer something to avoid for large project schedules.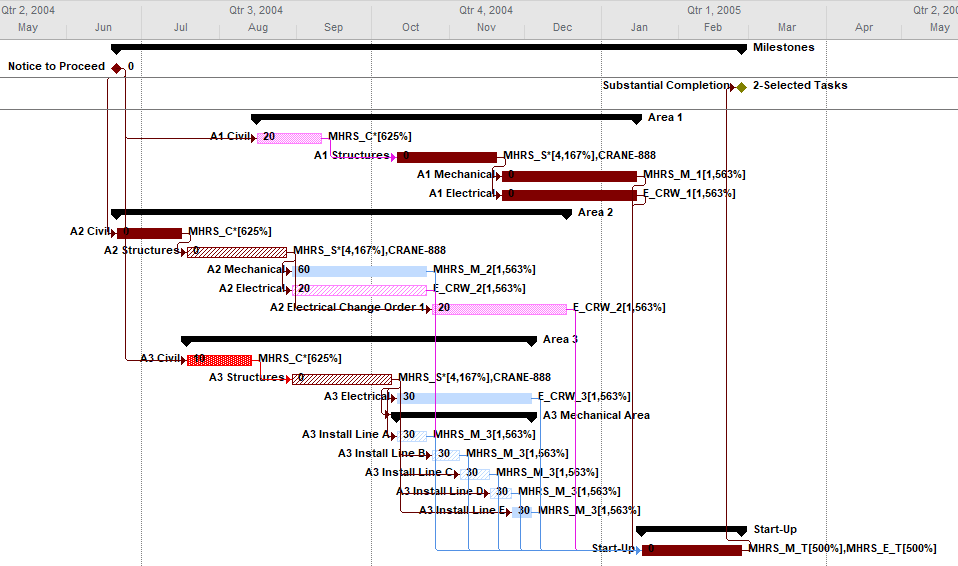
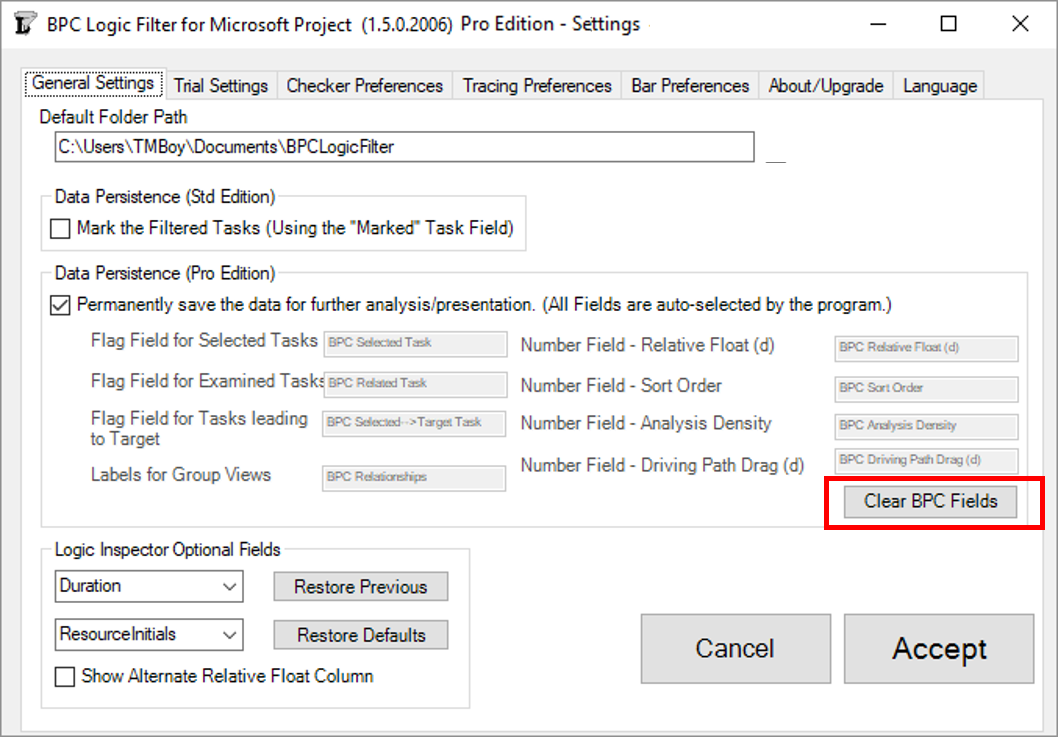
The new option does come at a cost, however. Specifically, it uses 4 more custom Flag fields (in addition to the 3 needed for generating filtered views). Custom fields typically get used up during the execution of a project, and constraining the need for custom fields was one of our key priorities during the early development of BPC Logic Filter. This new demand may force schedulers to be a bit more disciplined in allocating them. The accelerated bar coloring process also has a more rigid requirement for Data Persistence. If “Permanently save the data for further analysis/presentation” is NOT checked, then none of the important information will be shown. (With both the acceleration and permanently-save options turned off, bars are correctly colored, but logic-related text is not shown.) Finally, the additional overhead imposed by the setting can actually slow down the overall analysis and display of a smaller project schedule, so it is not always the fastest.
Link Options
All previous versions of BPC Logic Filter have automatically enforced the inclusion of end-connected link lines (relationship lines) in logic tracing results. The new version leaves this selection to the user.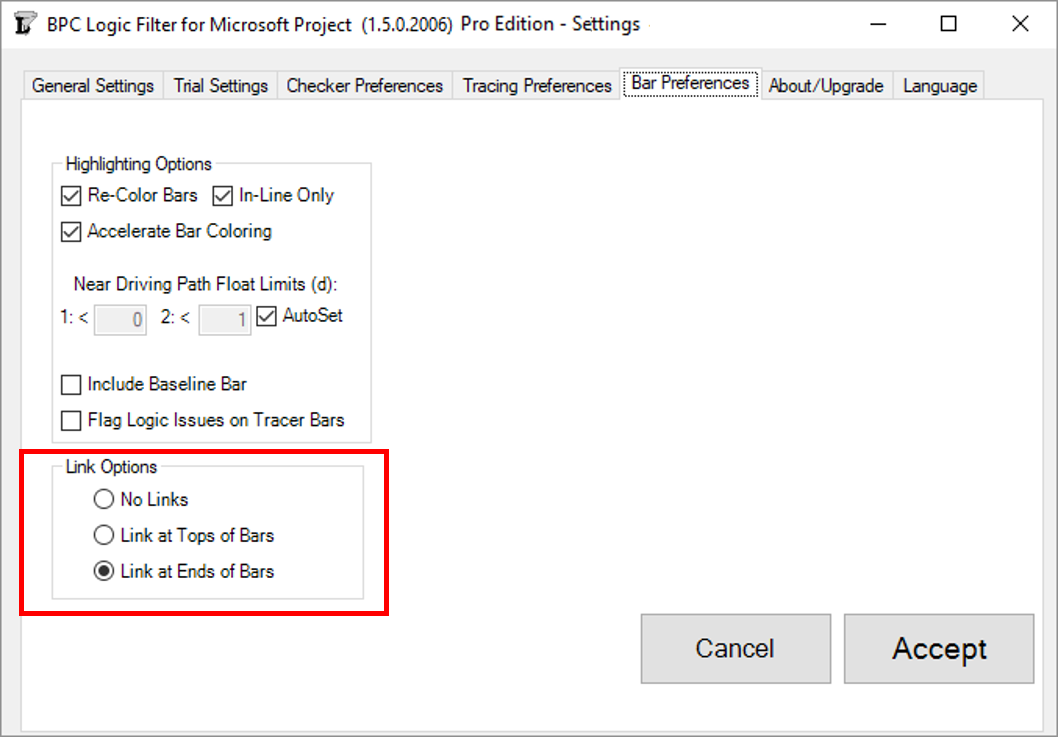
Logic-Jumping Through Hidden Tasks
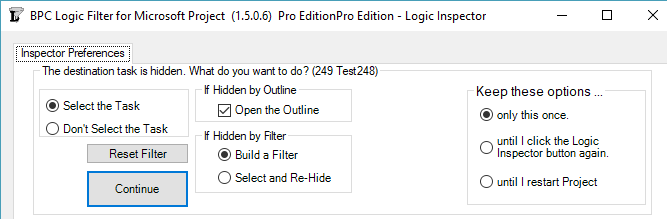
As any user of MSP’s built-in “Go To” (F5) tool knows, a task must be visible in the existing view to be selected and activated. In the past, this meant that the Logic Inspector Jump buttons – used for navigating through the schedule based on logic relationships alone – could be blocked if portions of the schedule were hidden (by filters or outlining). In the last build of version 1.4, we introduced some features for automatically breaking through such blockages.
Version 1.5 refines and provides for user-control of the behavior. First, it is now possible to fully navigate through any project schedule using the Jump buttons alone, without selecting or activating the tasks in the corresponding task table. This is the behavior demonstrated by the first radio button in the new form below.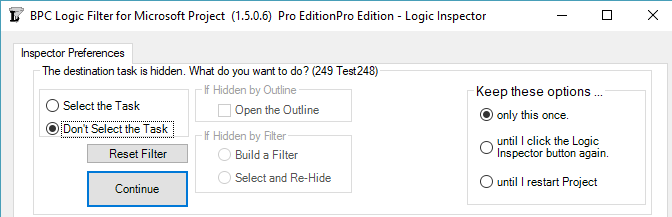
Alternately, the Logic Inspector can automatically select and activate the hidden task by opening a closed Outline (i.e. summary task) where necessary and by adding the task to a temporary filter. (Two types of filter persistence are supported.)
The new form is presented on the first attempt to Jump to a hidden task. The options on the left side of the form tell the software how to handle the specific hidden task. The buttons on the right side tell the software how long to remember this selection. You can always change this decision using the “Reset Filter” button in the Settings.
Streamlined Code and Improved Housekeeping
In addition to the improvements noted above, Version 1.5 incorporates substantial changes to the underlying code base, leading to faster and more efficient analyses.
As a minor note, there is another new user control provided in the General Settings dialog: the “Clear BPC Fields” button. This allows the permanent removal of all BPC-related custom field names and associated data.