Mandatory waiting times between certain tasks are a common feature of many project schedules. In construction, the typical example is concrete curing time. That is the time interval (typically under a week) after a batch of concrete is placed but before it gains sufficient strength to remove/strip the formwork and continue working. Similar wait times can be required in non-construction projects. Common features of such waiting times are:
- The waiting time is not associated with productive work;
- The waiting time is independent of any Project, Task, or Resource calendar. That is, it takes place around the clock, independent of weekends and holidays.
Consider a 5-day curing time in a Microsoft Project (MSP) schedule using the default Standard calendar (i.e. 5dx8h Monday-Friday work week). The curing process always occurs over a mix of working and non-working (night and weekend) time. Since the number of workdays included in this period varies from three to five depending on the time and day of the week that the concrete placement finishes, it is not possible to specify a fixed curing duration (in Standard-calendar workdays) without introducing an unnecessary delay in the schedule.
Instead, there are four obvious modeling techniques to accurately schedule the curing and follow-on activities:
- Create a “cure” task with a “5-day” duration and assign a 7-day x 24-hour calendar to the task.

- Create a “cure” task and assign a duration of 5 “elapsed” days.

- Don’t create a “cure” task. Instead model the curing time as a 5-elapsed-day lag between the “place concrete” and “strip forms” tasks.

- Create a “cure” task with a 5-day duration and assign a modified 7-day weekly calendar to the task.

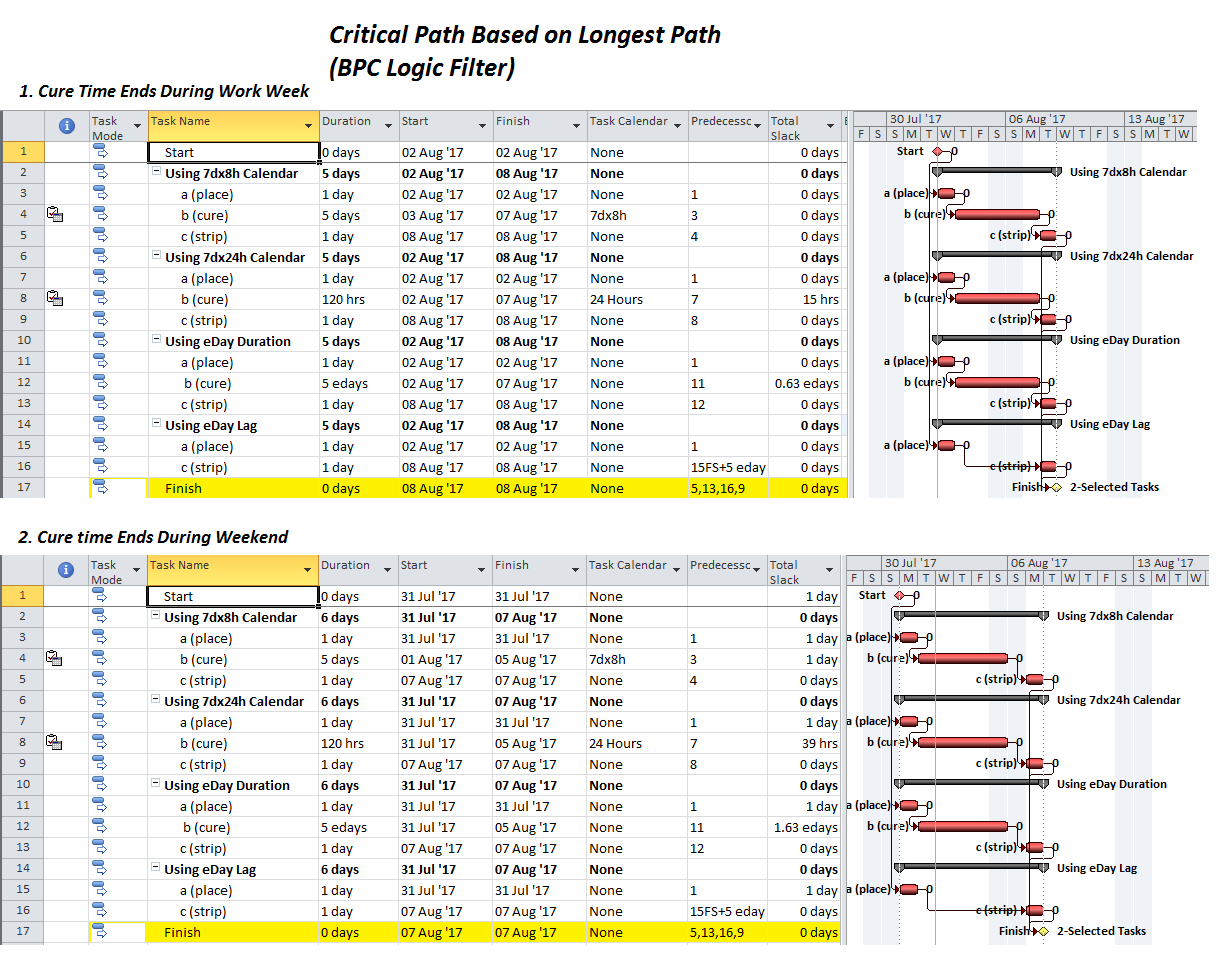
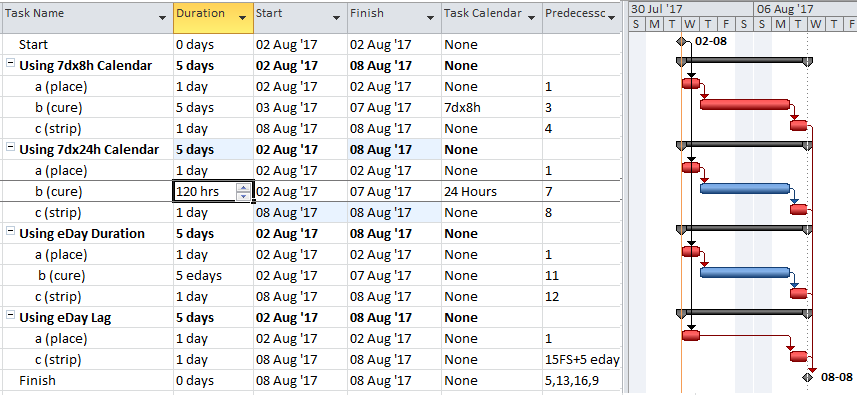
As shown in the figures, all four techniques can be used to generate the same (early) schedule dates for the project. Which technique to use depends on a few factors.
- Within MSP, a “day” is fundamentally defined according to the “hours per day” setting for the project, and any “day” entries are automatically converted to minutes using that setting. With default settings, one “day” is 8 hours (i.e. 480 minutes). This can lead to confusion when calendars are changed or assigned without taking the setting into account. For example, when a 24-hour calendar is assigned to a 3-day-duration task in a project with default (i.e. 8 hours/day) settings, then the task will finish in 24 hours (i.e. 1 calendar day). Under the same conditions, a curing time of 5 calendar days (i.e. 120 hours) would require a specified task “duration” of 120/8 = 15 days. To minimize such confusion, it is a good practice to specify durations in hours when 24-hour calendars are applied, as shown in the figure.
- For most purposes, assigning an “elapsed days” duration is functionally equivalent to applying a 24-hour calendar to the task and making the necessary duration adjustments. This can reduce confusion associated with the hours per day setting. The two techniques yield identical results in the example.
- Using an elapsed-lag instead of a dedicated task is functionally simple to implement, and many project schedulers routinely use this approach. Nevertheless, lags are generally discouraged or prohibited by some scheduling specifications and recommended practices for good reasons. Chiefly, lags can substantially affect schedule dates while remaining relatively invisible on typical schedule documents – this makes them easy to abuse for date-manipulation. In addition, unlike tasks, lags are not easily incorporated into external algorithms for evaluation or manipulation of project schedules – e.g. for risk simulation. This can substantially degrade the value of such algorithms.
- Total Slack calculations are substantially complicated by the impacts of multiple calendars (including the use of elapsed durations). Since MSP relies solely on Total Slack to identify “Critical” tasks, the true Critical Path for the project can be inadequately described for any of these techniques. For example, when the curing time finishes at the end of a workday in the middle of the work week, the “cure” task (on a 24-hour calendar) possesses 15 hours of Total Slack – MSP therefore excludes it from the Critical Path. If instead of a 24-hour calendar, a modified (i.e. 7d x 8h, no-weekend) calendar is applied to the curing task, then the positive Total Slack is eliminated in this case, and the Critical Path is correct. (This is shown at the top of the figure below.) Unfortunately, the modified calendar is no better than the others if the curing time finishes on the weekend. The 1 day of Total Slack causes the Critical Path to be truncated. (See the lower half of the figure below.)
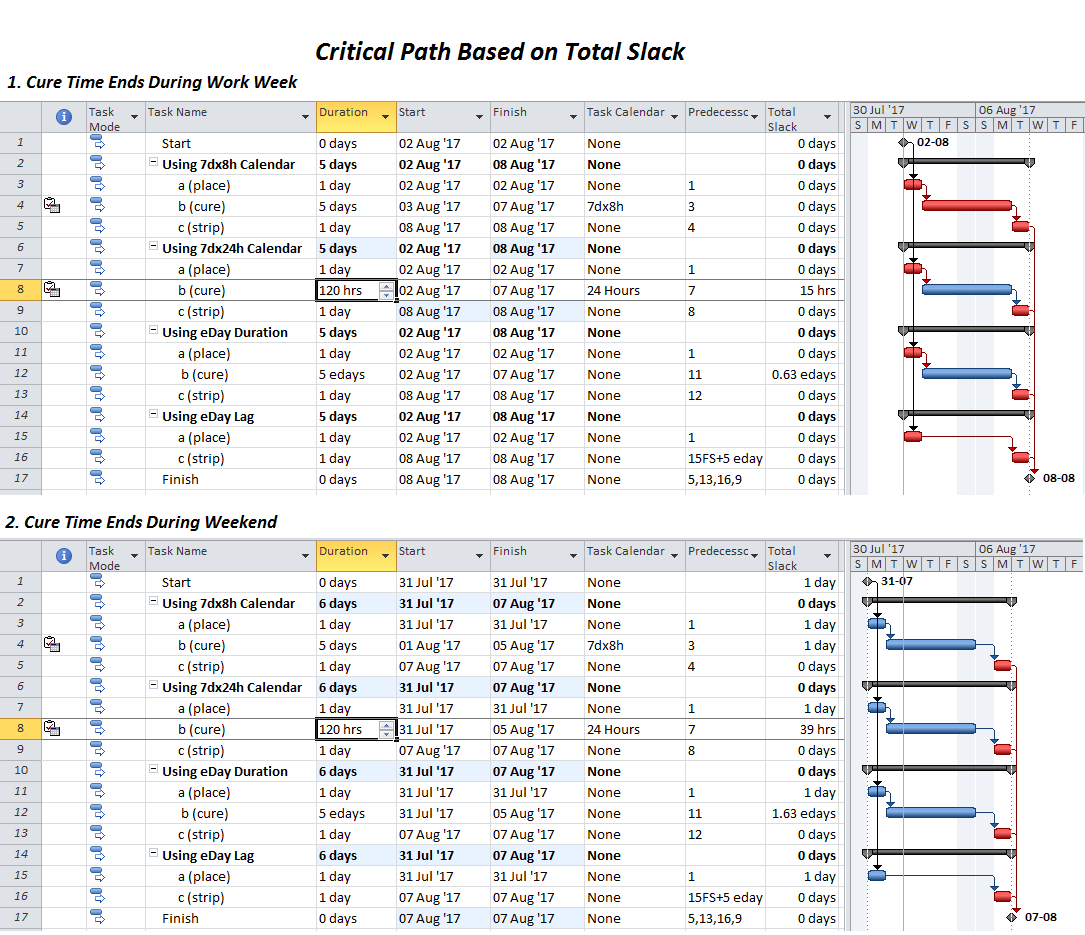
Unfortunately, the only out-of-the-box method to ensure that the entire critical path is captured is to raise the Total Slack threshold from the default value (zero) to some number that is judged high enough to capture all the truly critical tasks. I have found such an approach unsatisfactory for a variety of reasons. In any case, the true Critical Path – i.e. the driving logical path to project completion – remains obscured.
Fortunately, the Longest Path algorithm in BPC Logic Filter is indifferent to which modeling approach is used. As shown in the figure below, the driving logical paths are correctly identified for each case. (The number to the right of each bar is the task’s path relative float with respect to the project completion task – zero for the longest path. BPC Logic Filter typically depicts logical driving paths with a dark red bar.)